《2025年作业本江西教育出版社八年级数学上册人教版》

1.将含30°角的直角三角尺和直尺按如图所示的方式放置.若∠α= 60°,点B,C表示的刻度分别为1 cm,3 cm,则线段AB的长为2cm.

答案： 2

2.如图所示,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论：①AD= BE;②PQ//AE;③OP= OQ;④△CPQ为等边三角形;⑤∠AOB= 60°.其中正确的有①②④⑤(填序号).

答案： 证明：①
∵△ABC和△CDE是等边三角形，
∴AC=BC，CD=CE，∠ACB=∠DCE=60°，
∴∠ACB+∠BCD=∠DCE+∠BCD，即∠ACD=∠BCE，
在△ACD和△BCE中，
AC=BC，∠ACD=∠BCE，CD=CE，
∴△ACD≌△BCE（SAS），
∴AD=BE；
②由①得△ACD≌△BCE，
∴∠CAD=∠CBE，
∵∠ACB=∠DCE=60°，
∴∠BCD=60°，
在△ACP和△BCQ中，
∠CAP=∠CBQ，AC=BC，∠ACP=∠BCQ=60°，
∴△ACP≌△BCQ（ASA），
∴CP=CQ，
∵∠PCQ=60°，
∴△CPQ是等边三角形，
∴∠PQC=60°=∠DCE，
∴PQ//AE；
④由②得CP=CQ，∠PCQ=60°，
∴△CPQ为等边三角形；
⑤由①得△ACD≌△BCE，
∴∠ADC=∠BEC，
∴∠AOB=∠DAE+∠BEC=∠DAE+∠ADC=∠DCE=60°；
③假设OP=OQ，
∵PQ//AE，
∴∠OPQ=∠OAE，∠OQP=∠OEA，
∵△CPQ是等边三角形，
∴PQ=CQ，
但无法证明△OPQ中OP=OQ，故③错误。
正确的有①②④⑤。
答案：①②④⑤

3.如图所示,P是等边三角形ABC内一点,将△ABP绕点B按顺时针方向旋转60°,得到△CBP'.若PB= 3,则PP'= 3.

答案： 【解析】：本题可根据等边三角形的判定和性质来求解$PP'$的长度。
步骤一：分析$\triangle BPP'$的特征
已知$\triangle ABP$绕点$B$按顺时针方向旋转$60^{\circ}$得到$\triangle CBP'$，根据旋转的性质可知，旋转前后对应线段相等，对应角相等。
所以$BP = BP'$，且旋转角$\angle PBP' = 60^{\circ}$。
步骤二：判断$\triangle BPP'$的形状
在$\triangle BPP'$中，因为$BP = BP'$，$\angle PBP' = 60^{\circ}$，根据“有一个角是$60^{\circ}$的等腰三角形是等边三角形”，可以得出$\triangle BPP'$是等边三角形。
步骤三：计算$PP'$的长度
由于$\triangle BPP'$是等边三角形，根据等边三角形的性质：等边三角形的三条边都相等，已知$PB = 3$，所以$PP' = PB = 3$。
【答案】：$3$

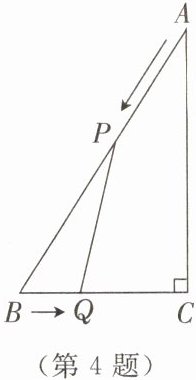
4.如图所示,在△ABC中,∠C= 90°,∠A= 30°,AB= 60 cm.动点P,Q同时从A,B两点出发,分别在AB,BC边上匀速移动,点P的运动速度为2 cm/s,点Q的运动速度为1 cm/s.当点P到达点B时,P,Q两点同时停止运动.设点P的运动时间为t s.
(1)当t为何值时,△PBQ为等边三角形?
(2)当t为何值时,△PBQ为直角三角形?

答案： 解：
(1)在$\triangle ABC$中，$\angle C = 90^{\circ}$，$\angle A = 30^{\circ}$，
$\therefore \angle B = 60^{\circ}$。
$\because 60÷2 = 30(s)$，
$\therefore 0\leqslant t\leqslant30$，
$BP=(60 - 2t)cm$，
$BQ = tcm$。
当$BP = BQ$时，$\triangle PBQ$为等边三角形，
即$60 - 2t = t$，$\therefore t = 20$。
当$t = 20$时，$\triangle PBQ$为等边三角形。
(2)若$\triangle PBQ$为直角三角形。
①当$\angle BQP = 90^{\circ}$时，$BP = 2BQ$。
即$60 - 2t = 2t$，$\therefore t = 15$。
②当$\angle BPQ = 90^{\circ}$时，$BQ = 2BP$。
即$t = 2(60 - 2t)$，$\therefore t = 24$。
即当$t = 15$或$t = 24$时，$\triangle PBQ$为直角三角形。