《2025年作业本江西教育出版社八年级数学上册人教版》

1. 下列变形中,错误的是______①②③(填序号).
①$(b-4c)^2= b^2-16c^2$；②$(a-2bc)^2= a^2+4abc+4b^2c^2$；③$(x+y)^2= x^2+xy+y^2$；④$(4m-n)^2= 16m^2-8mn+n^2$.

答案： 【解析】：
本题考察的是对完全平方公式的理解和应用。
完全平方公式为：$(a+b)^2 = a^2 + 2ab + b^2$ 和 $(a-b)^2 = a^2 - 2ab + b^2$。
需要逐一检查每个变形是否符合完全平方公式的形式。
① $(b-4c)^2$ 应该是 $b^2 - 2 × b × 4c + (4c)^2 = b^2 - 8bc + 16c^2$，
与给出的 $b^2 - 16c^2$ 不符，所以①是错误的。
② $(a-2bc)^2$ 应该是 $a^2 - 2 × a × 2bc + (2bc)^2 = a^2 - 4abc + 4b^2c^2$，
与给出的 $a^2 + 4abc + 4b^2c^2$ 不符，所以②是错误的。
③ $(x+y)^2$ 应该是 $x^2 + 2xy + y^2$，
与给出的 $x^2 + xy + y^2$ 不符，所以③是错误的。
④ $(4m-n)^2$ 应该是 $(4m)^2 - 2 × 4m × n + n^2 = 16m^2 - 8mn + n^2$，
与给出的 $16m^2 - 8mn + n^2$ 符合，所以④是正确的。
综上，错误的变形是①，②，③。
【答案】：
①②③

2. 如果$x^2 - 4(m - 1)x + 16$是一个完全平方式,那么$m= $$-1$或$3$.

答案： 解：因为$x^2 - 4(m - 1)x + 16$是完全平方式，所以$x^2 - 4(m - 1)x + 16=(x\pm4)^2$。
$(x + 4)^2=x^2 + 8x + 16$，则$-4(m - 1)=8$，解得$m - 1=-2$，$m=-1$。
$(x - 4)^2=x^2 - 8x + 16$，则$-4(m - 1)=-8$，解得$m - 1=2$，$m=3$。
综上，$m=-1$或$3$。

3. 计算：
(1)$(x+1)^2=$$x^2+2x+1$；
(2)$(-3x+1)^2=$$9x^2-6x+1$；
(3)$(-2a - b)^2=$$4a^2+4ab+b^2$.

答案：
(1)解：$(x+1)^2=x^2+2\cdot x\cdot1+1^2=x^2+2x+1$
(2)解：$(-3x+1)^2=(-3x)^2+2\cdot(-3x)\cdot1+1^2=9x^2-6x+1$
(3)解：$(-2a - b)^2=(-2a)^2+2\cdot(-2a)\cdot(-b)+(-b)^2=4a^2+4ab+b^2$

4. 计算：
(1)$\left(3a - \frac{1}{2}b\right)^2 - \left(3a + \frac{1}{2}b\right)^2$；
(2)$(x + 2)^2(x - 2)^2$；
(3)$4(x + 1)^2 - (2x + 5)(2x - 5)$；
(4)$9999^2$.

答案： 【解析】：
本题主要考察完全平方公式和平方差公式的运用。
(1) 可以利用平方差公式$a^2 - b^2 = (a + b)(a - b)$进行化简；
(2) 可以先利用平方差公式化简，再利用完全平方公式展开；
(3) 需要先分别展开两个平方项，然后合并同类项；
(4) 可以将$9999$表示为$(10000 - 1)$，然后利用完全平方公式进行化简。
【答案】：
解：
(1)
$\begin{aligned}\left(3a - \frac{1}{2}b\right)^2 - \left(3a + \frac{1}{2}b\right)^2 &= \left[\left(3a - \frac{1}{2}b\right) + \left(3a + \frac{1}{2}b\right)\right]\left[\left(3a - \frac{1}{2}b\right) - \left(3a + \frac{1}{2}b\right)\right] \\&= (6a)(-b) \\&= -6ab\end{aligned}$
(2)
$\begin{aligned}(x + 2)^2(x - 2)^2 &= \left[(x + 2)(x - 2)\right]^2 \\&= (x^2 - 4)^2 \\&= x^4 - 8x^2 + 16\end{aligned}$
(3)
$\begin{aligned}4(x + 1)^2 - (2x + 5)(2x - 5) &= 4(x^2 + 2x + 1) - (4x^2 - 25) \\&= 4x^2 + 8x + 4 - 4x^2 + 25 \\&= 8x + 29\end{aligned}$
(4)
$\begin{aligned}9999^2 &= (10000 - 1)^2 \\&= 10000^2 - 2 × 10000 × 1 + 1^2 \\&= 100000000 - 20000 + 1 \\&= 99980001\end{aligned}$

5. 先化简,再求值：$(a - 2b)(a + 2b) - (a - 2b)^2 + 8b^2$,其中$a= -2$,$b= \frac{1}{2}$.

答案： 解：原式$=a^2 - (2b)^2 - (a^2 - 4ab + 4b^2) + 8b^2$
$=a^2 - 4b^2 - a^2 + 4ab - 4b^2 + 8b^2$
$=4ab$
当$a=-2$，$b=\frac{1}{2}$时，
原式$=4×(-2)×\frac{1}{2}=-4$

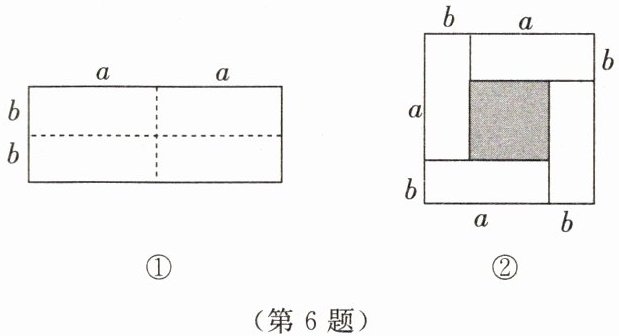
6. 图①是一个长为$2a$,宽为$2b$的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.

(第6题)
(1)图②中阴影部分的正方形的边长是______$a - b$______.
(2)用两种不同的方法求图②中阴影部分的面积：
方法1：______$(a - b)^2$______；
方法2：______$(a + b)^2 - 4ab$______.
(3)观察图②,请你写出式子$(a + b)^2$,$(a - b)^2$,$ab$之间的等量关系：______$(a + b)^2 - 4ab=(a - b)^2$______.
(4)根据(3)中的等量关系解决问题：若$m - n= -7$,$mn= 5$,则$(m + n)^2$的值为多少？69

答案： 【解析】：
(1)观察图②，阴影部分的正方形边长是长为$a$，宽为$b$的长方形的长与宽的差，即$(a - b)$。
(2)
方法1：根据正方形面积公式，阴影部分正方形边长为$(a - b)$，所以面积$S = (a - b)^2$。
方法2：大正方形边长为$(a + b)$，根据正方形面积公式，大正方形面积$S_{大}=(a + b)^2$；四个小长方形面积之和为$4ab$，那么阴影部分面积等于大正方形面积减去四个小长方形面积，即$S=(a + b)^2 - 4ab$。
(3)由
(2)中两种方法求阴影部分面积可得$(a + b)^2 - 4ab=(a - b)^2$。
(4)已知$m - n = -7$，$mn = 5$，要求$(m + n)^2$的值。
根据$(a + b)^2 - 4ab=(a - b)^2$，这里$a=m$，$b = n$，则$(m + n)^2=(m - n)^2+4mn$。
把$m - n = -7$，$mn = 5$代入上式可得：$(m + n)^2=(-7)^2 + 4×5=49 + 20 = 69$。
【答案】：
(1)$a - b$；
(2)$(a - b)^2$；$(a + b)^2 - 4ab$；
(3)$(a + b)^2 - 4ab=(a - b)^2$；
(4)69