《2025年作业本江西教育出版社八年级数学上册人教版》

1. 下列图形是轴对称图形的是③④⑤(填序号).

答案： 【解析】：
题目考察轴对称图形的识别，轴对称图形是指一个图形关于某条直线对称，如果沿这条直线折叠，图形的两部分能够完全重合，则称这个图形为轴对称图形。
根据轴对称图形的特点和图中给出的图形，逐一判断每个图形是否为轴对称图形：
图形①：没有对称轴使其对称。
图形②：没有对称轴使其对称。
图形③：有对称轴，左右对称。
图形④：有对称轴，上下对称。
图形⑤：有多个对称轴。
【答案】：
③④⑤

2. 小明从镜子里看到镜子对面电子钟的像如图所示,实际时间是16:25:08.

答案： 16:25:08

3. 如图所示,将已知图形分别在格点图中补充成关于已知直线l,m,n,p为对称轴的轴对称图形.

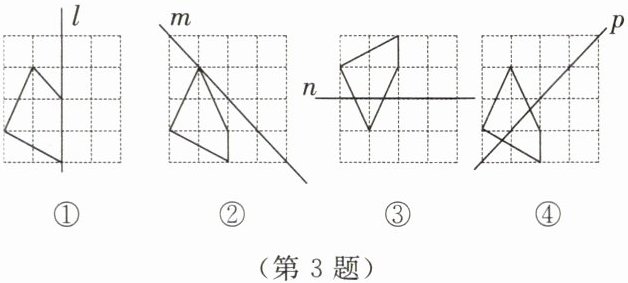
答案：

4. 如图所示,△ABC与△DEF关于直线MN对称,其中∠C= 90°.
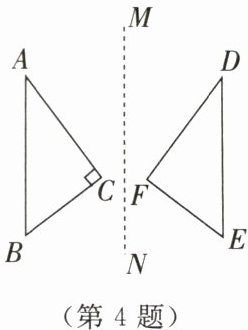
(1)点A与点D有何关系？连接AD,则线段AD与直线MN有何关系？
(2)求∠F的大小.

答案： 【解析】：
（1）根据对称点的定义，当两个图形关于某条直线对称时，对称点会落在该直线上或者关于该直线对称。由题可知，$\bigtriangleup ABC$与$\bigtriangleup DEF$关于直线$MN$对称，所以点$A$与点$D$作为两三角形的对应顶点，它们关于直线$MN$对称。连接$AD$，由于$A$和$D$关于$MN$对称，根据对称性质，线段$AD$会被直线$MN$垂直平分。
（2）由于$\bigtriangleup ABC$与$\bigtriangleup DEF$关于直线$MN$对称，根据对称性质，两个三角形的对应角相等。已知$\angle C=90^\circ$，因此$\angle F$作为$\bigtriangleup DEF$中与$\angle C$对应的角，其大小也应为$90^\circ$。
【答案】：
(1)点$A$与点$D$关于直线$MN$对称；线段$AD$被直线$MN$垂直平分。
(2)$\angle F=90^\circ$。

5. 如图所示,P为∠AOB内一点,分别作出P点关于OA,OB的对称点$P_1,P_2,$连接$P_1P_2$交OA于点M,交OB于点$N,P_1P_2= 15. $求△PMN的周长.

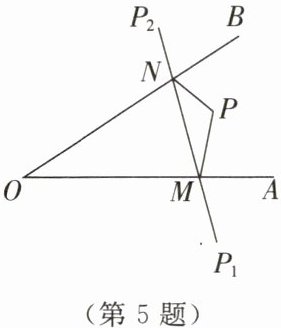
答案： 解：
∵P点关于OA的对称点为P₁，
∴PM = P₁M，
∵P点关于OB的对称点为P₂，
∴PN = P₂N，
∵△PMN的周长 = PM + MN + PN，
∴△PMN的周长 = P₁M + MN + P₂N = P₁P₂，
∵P₁P₂ = 15，
∴△PMN的周长为15。