《2025年作业本江西教育出版社八年级数学上册人教版》

1. 若等腰三角形的顶角为 $80^\circ$,则这个等腰三角形的底角为50$^\circ$.

答案： 解：设等腰三角形的底角为$x$。
因为等腰三角形两底角相等，三角形内角和为$180^\circ$，顶角为$80^\circ$，所以可得方程：
$2x + 80^\circ = 180^\circ$
$2x = 180^\circ - 80^\circ$
$2x = 100^\circ$
$x = 50^\circ$
故答案为：$50$

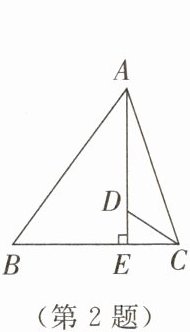
2. 如图所示,在 $\triangle ABC$ 中,$AC= BC$,$AE \perp BC$,垂足为 $E$,点 $D$ 在 $AE$ 上,且 $CD$ 平分 $\angle ACB$. 若 $\angle ABC= 54^\circ$,则 $\angle ADC= $126$^\circ$.

答案： 解：在△ABC中，AC=BC，
∴△ABC是等腰三角形，∠BAC=∠ABC=54°，
∠ACB=180°-∠BAC-∠ABC=180°-54°-54°=72°，
∵CD平分∠ACB，
∴∠ACD=∠BCD=∠ACB/2=72°/2=36°，
∵AE⊥BC，
∴∠AEC=90°，
在△DEC中，∠DCE=36°，∠DEC=90°，
∠EDC=180°-∠DCE-∠DEC=180°-36°-90°=54°，
∵∠ADC+∠EDC=180°（平角定义），
∴∠ADC=180°-∠EDC=180°-54°=126°。
126

3. 如图所示,直线 $l_1 // l_2$,点 $A$ 在直线 $l_1$ 上,点 $B$ 在直线 $l_2$ 上. 若 $AB= BC$,$\angle C= 30°$,$\angle 1= 80°$,则 $\angle 2= $40$°$.

答案： 180°-∠C-∠1=70°
∠2=70°-∠CAB=70°-∠C=40°

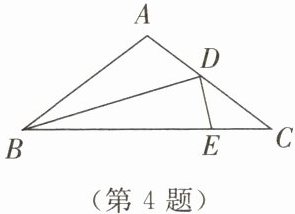
4. 如图所示,已知在 $\triangle ABC$ 中,$AB= AC$,$BD$ 是 $\angle ABC$ 的平分线,且 $BD= BE$,$\angle A= 100°$. 求 $\angle DEC$ 的大小.

答案： 解：在$△ABC$中，$AB=AC，$$∠A=100°，$　　
∴$∠ABC=∠C=\frac 12(180°-100°)=40°$　　
∵$BD$是$∠ABC$的平分线　　
∴$∠DBE=\frac 12∠ABC=20°$　　
∵$BD=BE$　　
∴$∠DEB=∠BDE=\frac 12(180°-∠DBE)=\frac 12×(180°-20°)=80°$　　
∴$∠DEC=180°-∠DEB=180°-80°=100°$　　

5. 一个等腰三角形的周长为 $28\ cm$.
(1)如果底边长是腰长的 $1.5$ 倍,求这个等腰三角形的三边长；
(2)如果一边长为 $10\ cm$,求这个等腰三角形另两边的长.

答案： 【解析】：
本题主要考查等腰三角形的性质以及一元一次方程的建立与求解。
(1) 设腰长为 $x \, cm$，则底边长为 $1.5x \, cm$。
由等腰三角形的周长公式 $2x + 底边 = 周长$，
代入已知条件得：
$2x + 1.5x = 28$
$3.5x = 28$
$x = 8$
所以，腰长为 $8 \, cm$，底边长为 $1.5 × 8 = 12 \, cm$。
(2) 对于一边长为 $10 \, cm$ 的情况，需要分两种可能讨论：
若 $10 \, cm$ 是腰长，则底边为 $28 - 10 × 2 = 8 \, cm$，另两腰长也为$10 \, cm$（等腰三角形的两腰相等），符合三角形三边关系（$10+10＞8$，$10+8＞10$，$8+10＞10$），所以另两边长为 $10 \, cm$，$8 \, cm$。
若 $10 \, cm$ 是底边，则腰长为 $\frac{28 - 10}{2} = 9 \, cm$，另两腰长都为 $9 \, cm$（等腰三角形的两腰相等），符合三角形三边关系（$9+9＞10$，$9+10＞9$，$10+9＞9$），所以另两边长为 $9 \, cm$，$9 \, cm$。
【答案】：
(1) 腰长为 $8 \, cm$，底边长为 $12 \, cm$。
(2) 另两边长为 $10 \, cm$，$8 \, cm$ 或 $9 \, cm$，$9 \, cm$。