《2025年作业本江西教育出版社八年级数学上册人教版》

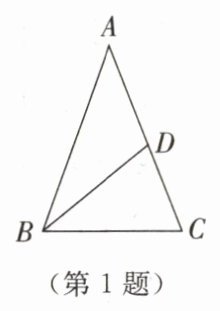
1. 如图所示,若 BD 是△ABC 的中线,AB= 5,BC= 3,且△ABD 的周长为 11,则△BCD 的周长是9.

答案： 解：
∵BD是△ABC的中线，
∴AD=CD。
∵△ABD的周长为11，AB=5，
∴AD+BD=11-AB=11-5=6。
∵BC=3，
∴△BCD的周长=BC+CD+BD=BC+(AD+BD)=3+6=9。

2. 如图所示,在△ABC 中,AC= 8,BC= 4,高 BD= 3,试作出 BC 边上的高 AE,并求 AE 的长.

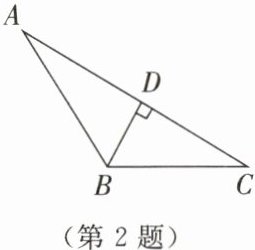
答案： 1. 首先，根据三角形面积公式$S = \frac{1}{2}ah$（$a$为底，$h$为这条底对应的高）：
对于$\triangle ABC$，以$AC$为底，$BD$为高时，其面积$S=\frac{1}{2}AC\cdot BD$；以$BC$为底，$AE$为高时，其面积$S = \frac{1}{2}BC\cdot AE$。
因为同一个三角形面积相等，即$S_{\triangle ABC}$是固定的。
2. 然后，根据面积相等列等式：
已知$AC = 8$，$BC = 4$，$BD = 3$。
由$\frac{1}{2}AC\cdot BD=\frac{1}{2}BC\cdot AE$（三角形面积公式的两种表示方法），两边同时约去$\frac{1}{2}$，得到$AC\cdot BD=BC\cdot AE$。
将$AC = 8$，$BC = 4$，$BD = 3$代入$AC\cdot BD=BC\cdot AE$中，可得$8×3 = 4× AE$。
解关于$AE$的方程：
根据等式的性质，$AE=\frac{8×3}{4}$。
先计算$8×3 = 24$，再计算$24÷4$，$AE = 6$。
解：因为$S_{\triangle ABC}=\frac{1}{2}AC\cdot BD=\frac{1}{2}BC\cdot AE$（三角形面积公式），所以$AC\cdot BD = BC\cdot AE$。
已知$AC = 8$，$BC = 4$，$BD = 3$，代入$8×3 = 4× AE$，得$AE=\frac{8×3}{4}=6$。
所以$AE$的长为$6$。

3. 如图所示,在△ABC 中(AB＞BC),AB= 2AC,AC 边上的中线 BD 把△ABC 的周长分成 30 和 20 两部分,求 AB 和 BC 的长.

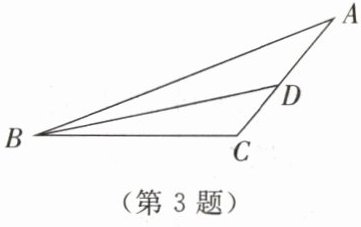
答案： 解：设 $ AC = x $，则 $ AB = 2x $。
∵ $ BD $ 是 $ AC $ 边上的中线，
∴ $ AD = DC = \frac{1}{2}AC = \frac{x}{2} $。
情况1： $ AB + AD = 30 $，$ BC + DC = 20 $
则 $ 2x + \frac{x}{2} = 30 $，解得 $ x = 12 $。
∴ $ AC = 12 $，$ AB = 2x = 24 $，$ DC = \frac{x}{2} = 6 $。
∴ $ BC = 20 - DC = 20 - 6 = 14 $。
此时 $ AB = 24 $，$ BC = 14 $，$ AC = 12 $，满足三角形三边关系。
情况2： $ AB + AD = 20 $，$ BC + DC = 30 $
则 $ 2x + \frac{x}{2} = 20 $，解得 $ x = 8 $。
∴ $ AC = 8 $，$ AB = 2x = 16 $，$ DC = \frac{x}{2} = 4 $。
∴ $ BC = 30 - DC = 30 - 4 = 26 $。
此时 $ AB = 16 $，$ BC = 26 $，$ AC = 8 $，
∵ $ 16 + 8 = 24 ＜ 26 $，不满足三角形三边关系，舍去。
综上，$ AB = 24 $，$ BC = 14 $。
答案：$ AB = 24 $，$ BC = 14 $。

4. 如图所示,在△ABC 中,BE 是角平分线,点 D 在边 AB 上(不与点 A,B 重合),CD 与 BE 交于点 O.
(1)若 CD 是中线,BC= 3,AC= 2,则△BCD 与△ACD 的周长的差为1；
(2)若 CD 是高,∠ABC= 62°,求∠BOC 的大小；

(3)若 CD 是角平分线,∠A= 78°,求∠BOC 的大小；

答案： 解：
(1)1
(2)
∵ BE 是 ∠ABC 的平分线，∠ABC = 62°，
∴ ∠ABE = $\frac{1}{2}$∠ABC = $\frac{1}{2}$×62° = 31°。
∵ CD 是 △ABC 的高，
∴ ∠CDB = 90°。
∵ ∠BOD = 180° - ∠DBO - ∠ODB = 180° - 31° - 90° = 59°，
∴ ∠BOC = 180° - ∠BOD = 180° - 59° = 121°。
(3) 在 △ABC 中，∠A = 78°，
∴ ∠ABC + ∠ACB = 180° - ∠A = 102°。
∵ BE 是 ∠ABC 的平分线，CD 是 ∠ACB 的平分线，
∴ ∠OBC = $\frac{1}{2}$∠ABC，∠OCB = $\frac{1}{2}$∠ACB，
∴ ∠OBC + ∠OCB = $\frac{1}{2}$(∠ABC + ∠ACB) = $\frac{1}{2}$×102° = 51°，
∴ ∠BOC = 180° - (∠OBC + ∠OCB) = 180° - 51° = 129°。