《2025年作业本江西教育出版社八年级数学上册人教版》

1. 如图所示,△ABC的边AB的垂直平分线交AC于点D,连接BD.若AC= 12,CD= 7,则BD= 5.

答案： 【解析】：本题可根据线段垂直平分线的性质来求解$BD$的长度。
线段垂直平分线的性质为：线段垂直平分线上的点到这条线段的两个端点的距离相等。
已知$DE$是$AB$的垂直平分线（设$DE$为$AB$垂直平分线），$D$在$DE$上，所以$AD = BD$。
又已知$AC = 12$，$CD = 7$，根据$AC=AD + CD$，可求出$AD$的长度，进而得到$BD$的长度。
【答案】：
解：
∵$DE$是$AB$的垂直平分线，$D$在$DE$上，
∴$AD = BD$。
∵$AC = 12$，$CD = 7$，且$AC=AD + CD$，
∴$AD=AC - CD=12 - 7 = 5$。
∵$AD = BD$，
∴$BD = 5$。
故答案为$5$。

2. 如图所示,线段AB,BC的垂直平分线$l_1,l_2$相交于点O.若∠B= 50°,则∠AOC= ______.

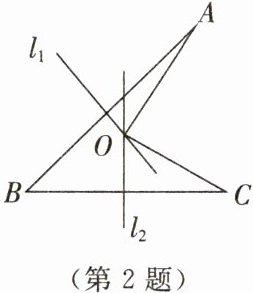
100°

答案： 解：连接OB。
∵l₁是AB的垂直平分线，
∴OA=OB，
∴∠OAB=∠OBA。
∵l₂是BC的垂直平分线，
∴OB=OC，
∴∠OBC=∠OCB。
∵∠ABC=∠OBA+∠OBC=50°，
∴∠OAB+∠OCB=50°。
在△ABC中，∠BAC+∠BCA=180°-∠ABC=130°，
∴∠OAC+∠OCA=∠BAC+∠BCA-(∠OAB+∠OCB)=130°-50°=80°。
在△AOC中，∠AOC=180°-(∠OAC+∠OCA)=180°-80°=100°。
100°

3. 如图所示,在△ABC中,AB= AC,BD⊥AC于点D,CE⊥AB于点E,BD,CE相交于点F.试判断AF所在的直线与BC的位置关系并说明理由.

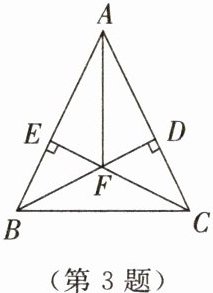
答案： 解：AF所在的直线垂直平分BC。
证明：
∵AB=AC，
∴∠ABC=∠ACB。
∵BD⊥AC，CE⊥AB，
∴∠BEC=∠CDB=90°。
在△BEC和△CDB中，
∠BEC=∠CDB，
∠EBC=∠DCB，
BC=CB，
∴△BEC≌△CDB（AAS）。
∴BE=CD。
∵AB=AC，
∴AB-BE=AC-CD，即AE=AD。
在△AEF和△ADF中，
AE=AD，
∠AEF=∠ADF=90°，
AF=AF，
∴△AEF≌△ADF（HL）。
∴∠BAF=∠CAF。
∵AB=AC，
∴AF所在的直线垂直平分BC（等腰三角形顶角的平分线与底边上的高、底边上的中线互相重合）。

证明：∵AD平分∠BAC,∴∠BAD= ∠DAC(角平分线的定义).∵EF垂直平分AD,∴FA= FD(线段垂直平分线上的点与这条线段两个端点的距离相等),∴∠BAD= ∠ADF(等边对等角),∴∠DAC= ∠ADF(等量代换),∴DF//AC(内错角相等，两直线平行).

答案： 【解析】：本题考查了角平分线的定义、线段垂直平分线的性质以及平行线的判定。
先根据角平分线的定义得到$\angle BAD=\angle DAC$。
再由线段垂直平分线的性质得出$FA = FD$，进而推出$\angle BAD=\angle ADF$。
最后通过等量代换得到$\angle DAC=\angle ADF$，根据内错角相等，两直线平行，证明$DF// AC$。
【答案】：证明：
∵$AD$平分$\angle BAC$，
∴$\angle BAD = \angle DAC$（角平分线的定义）。
∵$EF$垂直平分$AD$，
∴$FA = FD$（线段垂直平分线上的点与这条线段两个端点的距离相等），
∴$\angle BAD = \angle ADF$（等边对等角），
∴$\angle DAC = \angle ADF$（等量代换），
∴$DF// AC$（内错角相等，两直线平行）。