《2025年作业本江西教育出版社八年级数学上册人教版》

1. 在$\triangle ABC$中,若$\angle A= 80^\circ$,$\angle B= 50^\circ$,则$\angle C= $50$^\circ$.

答案： 解：在$\triangle ABC$中，
$\angle A + \angle B + \angle C = 180^\circ$（三角形内角和定理）
$\because \angle A = 80^\circ$，$\angle B = 50^\circ$
$\therefore \angle C = 180^\circ - \angle A - \angle B = 180^\circ - 80^\circ - 50^\circ = 50^\circ$
$50$

2. 在$\triangle ABC$中,若$\angle B= 2\angle A$,$\angle C= \angle A+40^\circ$,则$\angle A= $35°.

答案： 解：设∠A=x°，则∠B=2x°，∠C=(x+40)°。
因为三角形内角和为180°，
所以x + 2x + (x + 40) = 180，
4x + 40 = 180，
4x = 140，
x = 35。
故∠A=35°。

3. 如图所示,$\angle A= 75^\circ$,$\angle B= 65^\circ$,将纸片的一角折叠,使点C落在$\triangle ABC$的内部. 若$\angle 1= 45^\circ$,则$\angle 2= $35$^\circ$.

答案： 【解析】：
本题考查根据三角形内角和定理和折叠的性质来求$\angle 2$的度数。
步骤一：求出$\angle A+\angle B+\angle C$的度数
根据三角形内角和定理：三角形的内角和等于$180^{\circ}$，在$\triangle ABC$中，已知$\angle A = 75^{\circ}$，$\angle B = 65^{\circ}$，所以$\angle C=180^{\circ}-\angle A - \angle B=180^{\circ}-75^{\circ}-65^{\circ}=40^{\circ}$。
步骤二：分析折叠后角的关系
将纸片一角折叠使点$C$落在$\triangle ABC$内部，那么$\angle C'=\angle C = 40^{\circ}$（折叠前后对应角相等）。
在四边形$ABC'D$（设折痕与$AB$、$AC'$的交点等构成的四边形）中，$\angle A$、$\angle B$、$\angle C'$、$\angle 1+\angle 2$的和为$360^{\circ}$（四边形内角和为$360^{\circ}$）。
步骤三：计算$\angle 2$的度数
已知$\angle A = 75^{\circ}$，$\angle B = 65^{\circ}$，$\angle C' = 40^{\circ}$，$\angle 1 = 45^{\circ}$，代入$\angle A+\angle B+\angle C'+\angle 1+\angle 2 = 360^{\circ}$可得：
$75^{\circ}+65^{\circ}+40^{\circ}+45^{\circ}+\angle 2 = 360^{\circ}$
$\angle 2=360^{\circ}-(75^{\circ}+65^{\circ}+40^{\circ}+45^{\circ})$
$\angle 2=360^{\circ}-225^{\circ}=35^{\circ}$
【答案】：$35$

4. 已知三角形三个内角的大小比为1：3：5,求这三个内角的大小.

答案： 【解析】：
本题主要考察三角形内角和定理的应用。三角形三个内角的和为$180^\circ$。题目给出三个内角的比例为1：3：5，我们可以设三个内角分别为$x$，$3x$，$5x$。然后根据三角形内角和定理，列出方程求解。
【答案】：
解：设三角形的三个内角分别为$x$，$3x$，$5x$。
根据三角形内角和定理，有：
$x + 3x + 5x = 180^\circ$，
合并同类项，得：
$9x = 180^\circ$，
系数化为$1$，得：
$x = 20^\circ$，
所以，三角形的三个内角分别为：
$x = 20^\circ$，
$3x = 60^\circ$，
$5x = 100^\circ$，
答：三角形的三个内角的大小分别为$20^\circ$，$60^\circ$，$100^\circ$。

5. 如图所示,在$\triangle ABC$中,$BD\perp AC$于点D,AE是$\angle CAB$的平分线,交BD于点E. 若$\angle AEB= 120^\circ$,$\angle CBA= 40^\circ$,求$\angle C$的大小.

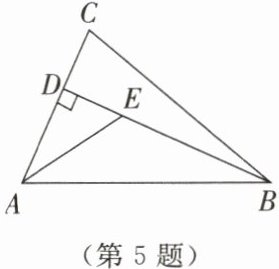
答案： 解：
∵ $ BD \perp AC $，
∴ $ \angle ADE = 90^\circ $。
在 $ \triangle ADE $ 中，$ \angle AEB = \angle DAE + \angle ADE $（三角形外角等于不相邻两内角之和），
∵ $ \angle AEB = 120^\circ $，$ \angle ADE = 90^\circ $，
∴ $ \angle DAE = \angle AEB - \angle ADE = 120^\circ - 90^\circ = 30^\circ $。
∵ $ AE $ 平分 $ \angle CAB $，
∴ $ \angle CAB = 2\angle DAE = 2 × 30^\circ = 60^\circ $。
在 $ \triangle ABC $ 中，$ \angle CAB + \angle CBA + \angle C = 180^\circ $（三角形内角和定理），
∵ $ \angle CAB = 60^\circ $，$ \angle CBA = 40^\circ $，
∴ $ \angle C = 180^\circ - \angle CAB - \angle CBA = 180^\circ - 60^\circ - 40^\circ = 80^\circ $。
答：$ \angle C $ 的大小为 $ 80^\circ $。

6. 如图所示,DE分别交$\triangle ABC$的边AB,AC于点D,E,交BC的延长线于点F. 若$\angle B= 64^\circ$,$\angle ACB= 75^\circ$,$\angle AED= 50^\circ$,求$\angle BDF$的大小.

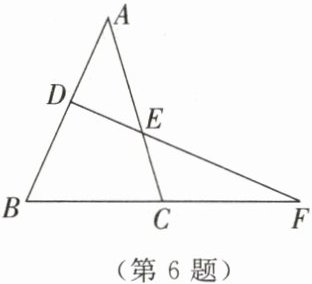
答案： 【解析】：
本题主要考查三角形内角和定理以及外角性质。
先根据三角形内角和定理求出$\angle A$的度数。
再利用三角形外角的性质求出$\angle BDF$的度数。
三角形内角和定理：三角形的内角和等于$180^\circ$。
三角形外角的性质：三角形的一个外角等于与它不相邻的两个内角之和。
【答案】：
解：
∵$\angle A + \angle B + \angle ACB = 180^\circ$（三角形内角和定理），
已知$\angle B = 64^\circ$，$\angle ACB = 75^\circ$，
∴$\angle A = 180^\circ - 64^\circ - 75^\circ = 41^\circ$。
∵$\angle BDF$是$\bigtriangleup ADE$的外角（三角形外角的定义），
∴$\angle BDF = \angle A + \angle AED$（三角形的一个外角等于与它不相邻的两个内角之和）。
已知$\angle AED = 50^\circ$，
∴$\angle BDF = 41^\circ + 50^\circ = 91^\circ$。
故答案为：$91^\circ$。