第17页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
1. 如图所示,已知线段a,b,用圆规和直尺作一条线段,使它等于3b-a.(保留作图痕迹,不写作法)
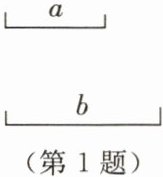

答案:
【解析】:本题主要考查了线段的基本作图,涉及到用圆规和直尺进行线段的加减法作图。要求作一条线段等于$3b - a$,需要先作出$3b$,再在$3b$上截取$a$的长度,从而得到$3b - a$。
【答案】:
解:图略(按照以下步骤作图)
1. 作射线$AM$。
2. 用圆规在射线$AM$上截取$AB = b$。
3. 不改变圆规两脚间的距离,依次在$AB$的延长线上截取$BC = b$,$CD = b$,此时$AD = 3b$。
4. 用圆规量取线段$a$的长度,在$AD$上从点$D$向点$A$方向截取$DE = a$,则线段$AE$就是所求作的线段,即$AE = 3b - a$。
【答案】:
解:图略(按照以下步骤作图)
1. 作射线$AM$。
2. 用圆规在射线$AM$上截取$AB = b$。
3. 不改变圆规两脚间的距离,依次在$AB$的延长线上截取$BC = b$,$CD = b$,此时$AD = 3b$。
4. 用圆规量取线段$a$的长度,在$AD$上从点$D$向点$A$方向截取$DE = a$,则线段$AE$就是所求作的线段,即$AE = 3b - a$。
2. 如图所示,已知∠BAC,作∠α等于∠BAC.(保留作图痕迹,不写作法)
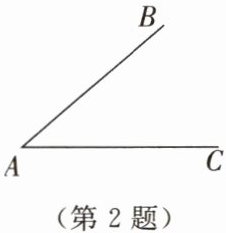

答案:
【解析】:本题考查尺规作图——作一个角等于已知角,需要用到的知识点为尺规作图的基本步骤和方法。
【答案】:解:
图略。
步骤如下:
1.以∠BAC的顶点A为圆心,任意长为半径画弧,分别交AB、AC于点D、E;
2.作射线OP,以O为圆心,AD长为半径画弧,交OP于点M;
3.用圆规量取DE的长,以M为圆心,DE长为半径画弧,交前弧于点N;
4.作射线ON,则∠PON即为所求作的∠α。
【答案】:解:
图略。
步骤如下:
1.以∠BAC的顶点A为圆心,任意长为半径画弧,分别交AB、AC于点D、E;
2.作射线OP,以O为圆心,AD长为半径画弧,交OP于点M;
3.用圆规量取DE的长,以M为圆心,DE长为半径画弧,交前弧于点N;
4.作射线ON,则∠PON即为所求作的∠α。
3. 如图所示,已知线段a,b和∠α,作△ABC,使BC= a,AC= b,∠BAC= ∠α.(保留作图痕迹,不写作法)
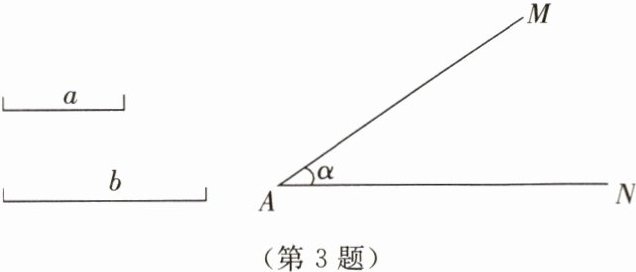

答案:
解:如图所示,△ABC或△AB'C即为所求作
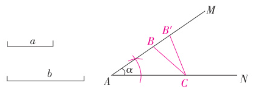
解:如图所示,△ABC或△AB'C即为所求作

4. (1)如图所示,已知△ABC,求作△A'B'C',使得△A'B'C'≌△ABC.写出作法.
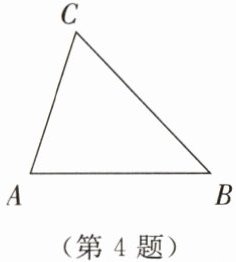
作法:
1. 作射线A'D;
2. 在射线A'D上截取A'B'=AB;
3. 以A'为顶点,A'D为一边,作∠DA'E=∠A;
4. 在射线A'E上截取A'C'=AC;
5. 连接B'C',则△A'B'C'即为所求。
(2)请你根据作图过程解答下列问题.
①完成下面证明过程.
证明:由作图可知,
在△A'B'C'和△ABC中,
$\left\{\begin{array}{l} A'B'= AB,\\ ∠DA'E= ∠(
∴△A'B'C'≌
②这种作一个三角形与已知三角形全等的方法的依据是
a. AAS;b. ASA;c. SAS;d. SSS.

作法:
1. 作射线A'D;
2. 在射线A'D上截取A'B'=AB;
3. 以A'为顶点,A'D为一边,作∠DA'E=∠A;
4. 在射线A'E上截取A'C'=AC;
5. 连接B'C',则△A'B'C'即为所求。
(2)请你根据作图过程解答下列问题.
①完成下面证明过程.
证明:由作图可知,
在△A'B'C'和△ABC中,
$\left\{\begin{array}{l} A'B'= AB,\\ ∠DA'E= ∠(
A
),\\ A'C'= (AC
),\end{array} \right.$∴△A'B'C'≌
△ABC
.②这种作一个三角形与已知三角形全等的方法的依据是
c
(填字母).a. AAS;b. ASA;c. SAS;d. SSS.
答案:
(1)作法:
1. 作射线A'D;
2. 在射线A'D上截取A'B'=AB;
3. 以A'为顶点,A'D为一边,作∠DA'E=∠A;
4. 在射线A'E上截取A'C'=AC;
5. 连接B'C',则△A'B'C'即为所求。
(2)①证明:由作图可知,
在△A'B'C'和△ABC中,
$\left\{\begin{array}{l} A'B'= AB,\\ ∠DA'E= ∠(A),\\ A'C'= (AC),\end{array} \right.$
∴△A'B'C'≌△ABC.
②c
(1)作法:
1. 作射线A'D;
2. 在射线A'D上截取A'B'=AB;
3. 以A'为顶点,A'D为一边,作∠DA'E=∠A;
4. 在射线A'E上截取A'C'=AC;
5. 连接B'C',则△A'B'C'即为所求。
(2)①证明:由作图可知,
在△A'B'C'和△ABC中,
$\left\{\begin{array}{l} A'B'= AB,\\ ∠DA'E= ∠(A),\\ A'C'= (AC),\end{array} \right.$
∴△A'B'C'≌△ABC.
②c
查看更多完整答案,请扫码查看


