第94页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. 离差平方和是各个数据与它们
平均数
之差的平方和;通常用$S^{2}$来表示,一组数据$x_{1},x_{2},…,x_{n}的平均数为\overline{x}$,则$S^{2}= $$(x_{1}-\overline {x})^{2}+(x_{2}-\overline {x})^{2}+·s +(x_{n}-\overline {x})^{2}$
。离差平方和是刻画数据离散程度
的一个统计量。
答案:
平均数 $(x_{1}-\overline {x})^{2}+(x_{2}-\overline {x})^{2}+\cdots +(x_{n}-\overline {x})^{2}$ 离散程度
2. 方差是各个数据与平均数之差的平方的
平均数
,通常用$s^{2}$来表示,一组数据$x_{1},x_{2},…,x_{n}的平均数为\overline{x}$,则$s^{2}= $$\frac {1}{n}[(x_{1}-\overline {x})^{2}+(x_{2}-\overline {x})^{2}+·s +(x_{n}-\overline {x})^{2}]$
。而标准差是方差的算术平方根
,通常用$s$来表示,$s= $$\sqrt {\frac {1}{n}[(x_{1}-\overline {x})^{2}+(x_{2}-\overline {x})^{2}+·s +(x_{n}-\overline {x})^{2}]}$
。一般而言,一组数据的方差或标准差越小
,这组数据就越稳定。
答案:
平均数 $\frac {1}{n}[(x_{1}-\overline {x})^{2}+(x_{2}-\overline {x})^{2}+\cdots +(x_{n}-\overline {x})^{2}]$ 算术平方根 $\sqrt {\frac {1}{n}[(x_{1}-\overline {x})^{2}+(x_{2}-\overline {x})^{2}+\cdots +(x_{n}-\overline {x})^{2}]}$ 小
1. 下列不能表示数据离散程度的量的是(
A.方差
B.离差平方和
C.平均数
D.标准差
C
)。A.方差
B.离差平方和
C.平均数
D.标准差
答案:
C
2. 甲、乙、丙、丁四位同学在四次数学测验中成绩的平均数相同,方差分别为$s_{甲}^{2}= 5.5$,$s_{乙}^{2}= 7.3$,$s_{丙}^{2}= 8.6$,$s_{丁}^{2}= 4.5$,则成绩最稳定的是(
A.甲同学
B.乙同学
C.丙同学
D.丁同学
D
)。A.甲同学
B.乙同学
C.丙同学
D.丁同学
答案:
D
3. 右图是小明和小华射箭的成绩统计图,两人都射了10次,射箭成绩的方差较小的是(
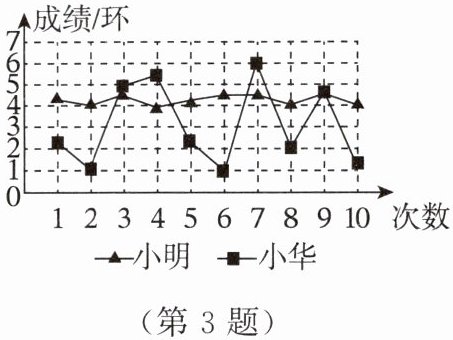
A.小华
B.小明
C.两人一样
D.无法确定
B
)。
A.小华
B.小明
C.两人一样
D.无法确定
答案:
B
4. 一组数据$4,5,a,6,8的平均数\overline{x}= 5$,则方差$s^{2}= $
4
。
答案:
4
5. 从甲、乙两种玉米苗中各抽10株,测得它们的株高分别如下(单位:cm):
甲:$25,41,40,37,22,14,19,39,21,42$;
乙:$27,16,44,27,44,16,40,40,16,40$。
(1)哪种玉米苗长得高?
(2)哪种玉米苗长得齐?
甲:$25,41,40,37,22,14,19,39,21,42$;
乙:$27,16,44,27,44,16,40,40,16,40$。
(1)哪种玉米苗长得高?
(2)哪种玉米苗长得齐?
答案:
(1)$\overline {x}_{甲}=\frac {1}{10}× (25+41+40+37+22+14+19+39+21+42)=\frac {1}{10}× 300=30(cm)$。$\overline {x}_{乙}=\frac {1}{10}× (27+16+44+27+44+16+40+40+16+40)=\frac {1}{10}× 310=31(cm)$。因为$\overline {x}_{甲}<\overline {x}_{乙}$,所以乙种玉米苗长得高。
(2)$s^{2}_{甲}=\frac {1}{10}× [(25-30)^{2}+(41-30)^{2}+\cdots +(42-30)^{2}]=\frac {1}{10}× 1042=104.2$。$s^{2}_{乙}=\frac {1}{10}× [(27-31)^{2}+(16-31)^{2}+\cdots +(40-31)^{2}]=\frac {1}{10}× 1288=128.8$。因为$s^{2}_{甲}<s^{2}_{乙}$,所以甲种玉米苗长得齐。
(1)$\overline {x}_{甲}=\frac {1}{10}× (25+41+40+37+22+14+19+39+21+42)=\frac {1}{10}× 300=30(cm)$。$\overline {x}_{乙}=\frac {1}{10}× (27+16+44+27+44+16+40+40+16+40)=\frac {1}{10}× 310=31(cm)$。因为$\overline {x}_{甲}<\overline {x}_{乙}$,所以乙种玉米苗长得高。
(2)$s^{2}_{甲}=\frac {1}{10}× [(25-30)^{2}+(41-30)^{2}+\cdots +(42-30)^{2}]=\frac {1}{10}× 1042=104.2$。$s^{2}_{乙}=\frac {1}{10}× [(27-31)^{2}+(16-31)^{2}+\cdots +(40-31)^{2}]=\frac {1}{10}× 1288=128.8$。因为$s^{2}_{甲}<s^{2}_{乙}$,所以甲种玉米苗长得齐。
查看更多完整答案,请扫码查看


