《2025年配套综合练习甘肃八年级数学上册北师大版》

4. 解方程组：
(1) $\begin{cases}x + y + z = 6,\\y - z = 4,\\x - y - 2z = 3;\end{cases} $
(2) $\begin{cases}x + y - z = 11,\\y + z - x = 5,\\z + x - y = 1。\end{cases} $

答案： $(1)$ 解方程组$\begin{cases}x + y + z = 6\\y - z = 4\\x - y - 2z = 3\end{cases}$
解：
由$y - z = 4$可得$y = z + 4$。
将$y = z + 4$代入$x + y + z = 6$，得$x+(z + 4)+z = 6$，即$x + 2z = 2$，所以$x = 2 - 2z$。
把$y = z + 4$，$x = 2 - 2z$代入$x - y - 2z = 3$，得$(2 - 2z)-(z + 4)-2z = 3$。
去括号：$2 - 2z - z - 4 - 2z = 3$。
移项：$-2z - z - 2z = 3 + 4 - 2$。
合并同类项：$-5z = 5$。
系数化为$1$：$z=-1$。
把$z = - 1$代入$y = z + 4$，得$y=-1 + 4 = 3$。
把$z = - 1$代入$x = 2 - 2z$，得$x = 2-2×(-1)=4$。
所以方程组$\begin{cases}x + y + z = 6\\y - z = 4\\x - y - 2z = 3\end{cases}$的解为$\begin{cases}x = 4\\y = 3\\z = - 1\end{cases}$。
$(2)$ 解方程组$\begin{cases}x + y - z = 11\\y + z - x = 5\\z + x - y = 1\end{cases}$
解：
将方程组中三个方程相加得：$(x + y - z)+(y + z - x)+(z + x - y)=11 + 5 + 1$。
去括号：$x + y - z + y + z - x + z + x - y = 17$。
合并同类项：$x + y + z = 17$ ④。
用④$-$第一个方程$x + y - z = 11$得：$(x + y + z)-(x + y - z)=17 - 11$。
去括号：$x + y + z - x - y + z = 6$，即$2z = 6$，解得$z = 3$。
用④$-$第二个方程$y + z - x = 5$得：$(x + y + z)-(y + z - x)=17 - 5$。
去括号：$x + y + z - y - z + x = 12$，即$2x = 12$，解得$x = 6$。
用④$-$第三个方程$z + x - y = 1$得：$(x + y + z)-(z + x - y)=17 - 1$。
去括号：$x + y + z - z - x + y = 16$，即$2y = 16$，解得$y = 8$。
所以方程组$\begin{cases}x + y - z = 11\\y + z - x = 5\\z + x - y = 1\end{cases}$的解为$\begin{cases}x = 6\\y = 8\\z = 3\end{cases}$。
综上，$(1)$的解为$\boldsymbol{\begin{cases}x = 4\\y = 3\\z = - 1\end{cases}}$；$(2)$的解为$\boldsymbol{\begin{cases}x = 6\\y = 8\\z = 3\end{cases}}$。

5. 为确保信息安全,信息需加密传输,发送方由明文→密文(加密)；接收方由密文→明文(解密)。已知加密规则为：明文$a$,$b$,$c对应密文a + 2b$,$2b + c$,$3c$。例如：明文$1$,$2$,$3对应密文5$,$7$,$9$。当接收方收到密文$14$,$9$,$15$时,则解密得到的明文为(B)。
A.$10$,$5$,$2$
B.$10$,$2$,$5$
C.$2$,$5$,$10$
D.$5$,$10$,$2$

答案： B

6. 如下表,从左到右在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,则第$2017$个格子中的数为(A)。

A.$3$
B.$2$
C.$0$
D.$-1$

答案： A

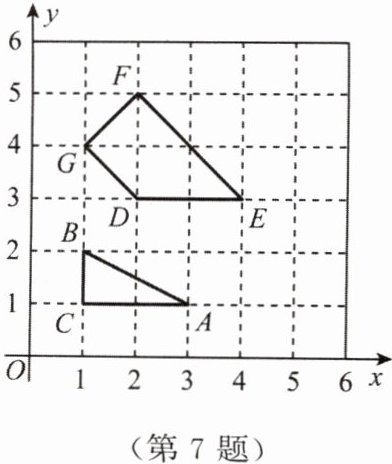
7. 在平面直角坐标系中,若点$P(x,y)的坐标x$,$y$均为整数,则称点$P$为格点。若一个多边形的面积记为$S$,其内部的格点数记为$N$,边界上的格点数记为$L$。例如,图中$\triangle ABC$是格点三角形,对应的$S = 1$,$N = 0$,$L = 4$。
(1) 求出图中格点四边形$DEFG对应的S$,$N$,$L$的值。
(2) 已知格点多边形的面积可表示为$S = N + aL + b$,其中$a$,$b$为常数。若某格点多边形对应的$N = 82$,$L = 38$,求$S$的值。

答案： 解:
(1)根据题图,可得$S=3,N=1,L=6$。
(2)根据格点三角形 ABC 及格点四边形 DEFG 对应的 S,N,L 的值可得,$\left\{\begin{array}{l} 4a+b=1,\\ 1+6a+b=3,\end{array}\right. $解得$\left\{\begin{array}{l} a=\frac{1}{2},\\ b=-1,\end{array}\right. $所以$S=N+\frac{1}{2}L-1$。将$N=82,L=38$代入上式,可得$S=82+\frac{1}{2}× 38-1=100$。