《2025年配套综合练习甘肃八年级数学上册北师大版》

7. 若代数式$\sqrt{x - 2}$有意义,则$x$的取值范围是(D)。
A.$x\gt2$
B.$x\lt2$
C.$x = 2$
D.$x\geqslant2$

答案： D

8. 若$\sqrt{a - 1}+b^{2}-4b + 4 = 0$,则$ab$的值为2。

答案： 2

9. 求一个正数的算术平方根,有些数可以直接求得,如$4的算术平方根是\sqrt{4}= 2$,有些数则不能直接求得,如$5的算术平方根是\sqrt{5}$,但可以通过计算器求得,有些数还可以通过一组数的内在联系,运用规律求得。请同学们观察下表：

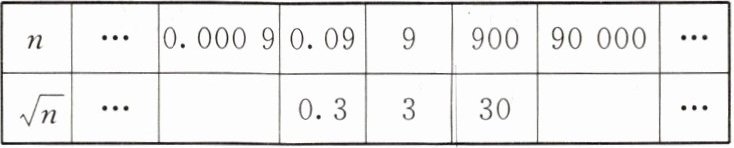
(1)根据表中所给的信息,观察规律,并将表格填写完整。
(2)运用你发现的规律,探究下列问题：已知$\sqrt{2.06}\approx1.435$,求下列各数的算术平方根的近似值：
①$0.0206$；
②$206$；
③$20600$。
(1)0.03 300 (2)①$\sqrt{0.0206}\approx0.1435$。②$\sqrt{206}\approx14.35$。③$\sqrt{20600}\approx143.5$。

答案： 解:
(1)0.03 300
(2)①$\sqrt{0.0206}\approx0.1435$。②$\sqrt{206}\approx14.35$。③$\sqrt{20600}\approx143.5$。

10. 先阅读下面提供的材料,再解答相应的问题：
若$\sqrt{x - 1}和\sqrt{1 - x}$都有意义,则$x$的值是多少？
解：因为$\sqrt{x - 1}和\sqrt{1 - x}$都有意义,
所以$x - 1\geqslant0且1 - x\geqslant0$。
又因为$x - 1和1 - x$互为相反数,而互为相反数的两个非负数均为$0$,
所以$x - 1 = 0且1 - x = 0$,
所以$x = 1$。
问题：若$y= \sqrt{2x - 1}+\sqrt{1 - 2x}+2$,则$x^{y}$的值是多少？

答案： 解:因为$\sqrt{2x-1}$和$\sqrt{1-2x}$都有意义,所以$2x-1\geq0$且$1-2x\geq0$。又因为$2x-1$和$1-2x$互为相反数,而互为相反数的两个非负数均为0,所以$2x-1=0$且$1-2x=0$,所以$x=\frac{1}{2}$,所以$y=2$。故$x^{y}=\left(\frac{1}{2}\right)^{2}=\frac{1}{4}$。