《2025年配套综合练习甘肃八年级数学上册北师大版》

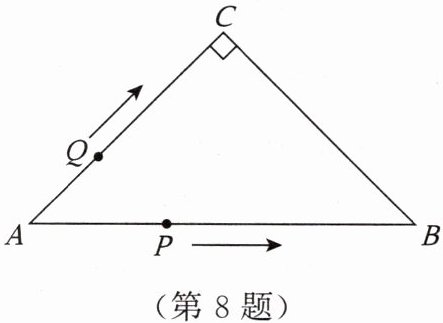
8. 如图,在 $ \triangle A B C $ 中,$ \angle C = 90 ^ { \circ } $,$ A C = B C = 3 cm $,动点 $ P $ 从点 $ A $ 出发,以 $ \sqrt { 2 } cm / s $ 的速度沿 $ A B $ 方向运动到点 $ B $,并停止运动,动点 $ Q $ 同时从点 $ A $ 出发,以 $ 1 cm / s $ 的速度沿折线 $ A - C - B $ 方向运动到点 $ B $,并停止运动,设 $ \triangle A P Q $ 的面积为 $ y cm ^ { 2 } $,点 $ Q $ 的运动时间为 $ x s $。
(1) 写出 $ y $ 与 $ x $ 之间的关系式,并写出自变量的取值范围；
(2) 若 $ \triangle A P Q $ 的面积为 $ 2 cm ^ { 2 } $,求 $ x $ 的值。

答案：
(1)如图①,当点Q在AC上运动时,$0\leqslant x\leqslant 3$,过点Q作$QD\perp AB$于点D,根据题意可知,$AQ=x\ cm$,$AP=\sqrt {2}x\ cm$,因为在$\triangle ABC$中,$\angle A=45^{\circ }$,所以$AD=DQ$。
在$Rt\triangle ADQ$中,由勾股定理可知$2QD^{2}=x^{2}$,
解得$QD=\frac {\sqrt {2}x}{2}\ cm$,于是$y=\frac {1}{2}× \sqrt {2}x× \frac {\sqrt {2}x}{2}=\frac {1}{2}x^{2}$。
如图②,当点Q在CB上运动时,$3＜x\leqslant 6$,此时点P与点B重合，过点Q作$QE\perp AB$于点E,由题意得$AC+CQ=x\ cm$,则$BQ=(6-x)\ cm$。
因为在$\triangle ABC$中,$\angle C=90^{\circ }$,$AC=BC=3\ cm$,
所以$\angle B=45^{\circ }$,$AB=AP=3\sqrt {2}\ cm$。
在$Rt\triangle BEQ$中,$2QE^{2}=(6-x)^{2}$,
于是$QE=\frac {\sqrt {2}}{2}(6-x)\ cm$,
所以$y=\frac {1}{2}× 3\sqrt {2}× \frac {\sqrt {2}}{2}(6-x)=-\frac {3}{2}x+9$。
综上所述,$y=\begin{cases} \frac{1}{2}x^{2}(0\leqslant x\leqslant 3),\\ -\frac{3}{2}x+9(3＜x\leqslant 6)。 \end{cases}$
(2)当$0\leqslant x\leqslant 3$时,令$\frac {1}{2}x^{2}=2$,解得$x=2$(负值已舍);
当$3＜x\leqslant 6$时,令$-\frac {3}{2}x+9=2$,解得$x=\frac {14}{3}$。
所以x的值为2或$\frac {14}{3}$。