第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. 在实际生产、生活中,常会碰到判断两条直线是否垂直的问题,即判断这两条直线构成的角是不是
2. 在确定线段长度的问题中,我们往往需要借助勾股定理,所以建立直角三角形的数学模型就显得非常重要。
直角
,若身边没有可以直接测量角的工具,只有测量线段的工具,我们可以在角的两条边上各取一点,连线,构造三角形,通过测量三条边的长度,再利用勾股定理的逆定理
来判断这个三角形是不是直角三角形,进而判断这个角是不是直角。2. 在确定线段长度的问题中,我们往往需要借助勾股定理,所以建立直角三角形的数学模型就显得非常重要。
答案:
1. 直角 勾股定理的逆定理
1. 如图,湖的两岸有$A$,$C$两点,在与$AC成直角的BC方向上的点B$处,测得$AB = 15m$,$BC = 12m$,则$A$,$C$两点之间的距离为(
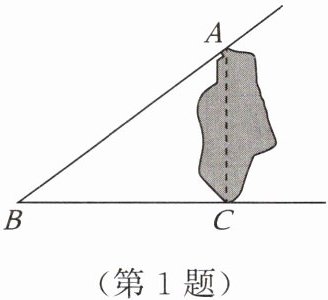
A.$3m$
B.$6m$
C.$9m$
D.$10m$
C
)。
A.$3m$
B.$6m$
C.$9m$
D.$10m$
答案:
C
2. 如图,从电线杆离地面$6m的地方拉一条10m$长的钢缆,地面上钢缆固定点$A到电线杆底部点B$的距离是(
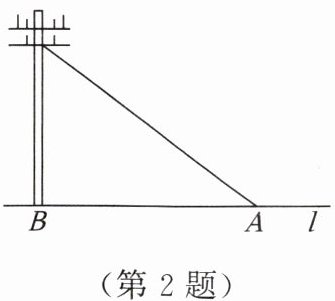
A.$6m$
B.$7m$
C.$8m$
D.$9m$
C
)。
A.$6m$
B.$7m$
C.$8m$
D.$9m$
答案:
C
3. 有一辆装货的汽车,为了方便装运货物,使用了如图所示的钢架,其中$\angle ACB = 90^{\circ}$,$AC = 1.2m$,$BC = 0.9m$,则$AB$的长为(
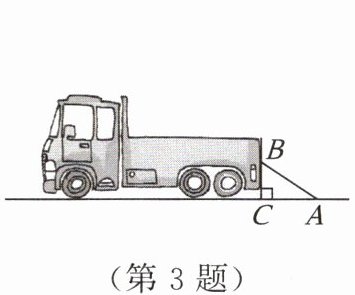
A.$1.2m$
B.$1.5m$
C.$1.8m$
D.$2m$
B
)。
A.$1.2m$
B.$1.5m$
C.$1.8m$
D.$2m$
答案:
B
查看更多完整答案,请扫码查看


