第69页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
7. 某健身俱乐部面向学生推出暑期优惠活动,活动方案如下。
方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠。
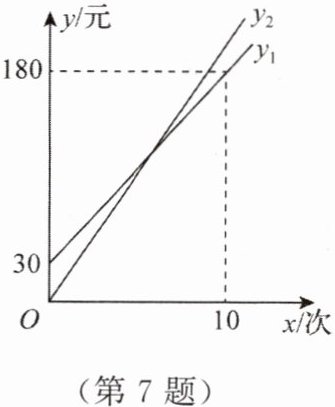
设某学生暑期健身$x$(次),按照方案一所需费用为$y_1$(元),且$y_1 = k_1x + b$;按照方案二所需费用为$y_2$(元),且$y_2 = k_2x$。其函数图象如图所示。
(1)求$k_1和b$的值,并说明它们的实际意义。
(2)求打折前的每次健身费用和$k_2$的值。
(3)八年级学生小华计划暑假期间前往该俱乐部健身$8$次,应选择哪种方案所需费用更少?说明理由。
]
方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠。
设某学生暑期健身$x$(次),按照方案一所需费用为$y_1$(元),且$y_1 = k_1x + b$;按照方案二所需费用为$y_2$(元),且$y_2 = k_2x$。其函数图象如图所示。
(1)求$k_1和b$的值,并说明它们的实际意义。
(2)求打折前的每次健身费用和$k_2$的值。
(3)八年级学生小华计划暑假期间前往该俱乐部健身$8$次,应选择哪种方案所需费用更少?说明理由。
]

答案:
(1)因为直线y₁=k₁x+b经过(0,30)和(10,180)两点,所以b=30,10k₁+b=180,则 k₁=15 ,b=30。k₁的实际意义是按六折优惠后的每次健身费用为15元,b的实际意义是一张学生暑期专享卡的价格为30元。
(2)因为每次健身费用按六折优惠后的费用为15元,所以打折前的每次健身费用为15÷0.6=25(元)。因为不购买学生暑期专享卡,每次健身费用按八折优惠,所以k₂=25×0.8=20。
(3)选择方案一所需费用更少。理由如下:当x=8时,y₁=15x+30=15×8+30=150,y₂=20x=20×8=160。因为150<160,所以选择方案一所需费用更少。
(1)因为直线y₁=k₁x+b经过(0,30)和(10,180)两点,所以b=30,10k₁+b=180,则 k₁=15 ,b=30。k₁的实际意义是按六折优惠后的每次健身费用为15元,b的实际意义是一张学生暑期专享卡的价格为30元。
(2)因为每次健身费用按六折优惠后的费用为15元,所以打折前的每次健身费用为15÷0.6=25(元)。因为不购买学生暑期专享卡,每次健身费用按八折优惠,所以k₂=25×0.8=20。
(3)选择方案一所需费用更少。理由如下:当x=8时,y₁=15x+30=15×8+30=150,y₂=20x=20×8=160。因为150<160,所以选择方案一所需费用更少。
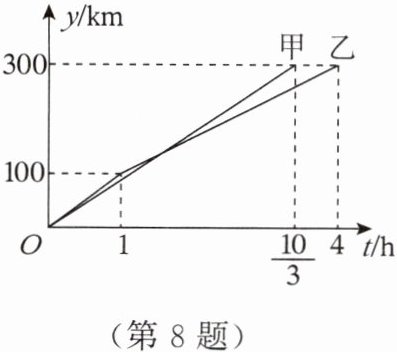
8. $A$,$B两地相距300km$,甲、乙两车同时从$A地出发前往B$地,如图所示的是甲、乙两车行驶路程$y(km)随行驶时间t(h)$变化的图象,结合图象信息,回答下列问题:
(1)甲车的速度为
(2)当甲、乙两车相距$10km$时,乙车行驶的时间为
]
(1)甲车的速度为
90
$km/h$;(2)当甲、乙两车相距$10km$时,乙车行驶的时间为
1或$\frac {13}{7}$或$\frac {77}{20}$
$h$。]

答案:
(1)90;
(2)1或$\frac {13}{7}$或$\frac {77}{20}$
(1)90;
(2)1或$\frac {13}{7}$或$\frac {77}{20}$
查看更多完整答案,请扫码查看


