《2025年名校课堂八年级数学上册人教版5四川专版》

1. 如图 1，把一张长方形纸片沿着线段 $ AB $ 剪开，把剪成的两张纸片拼成如图 2 所示的图形。


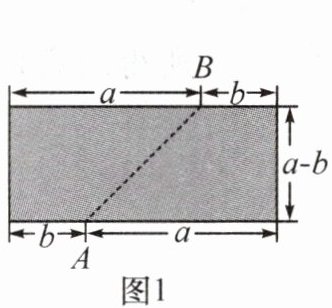
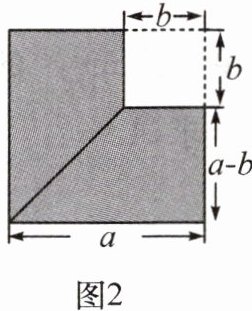
(1) 设图 1 中阴影部分的面积为 $ S_{1} $，图 2 中阴影部分的面积为 $ S_{2} $，请直接用含 $ a $，$ b $ 的式子表示 $ S_{1} $，$ S_{2} $。
(2) 请写出上述过程所揭示的乘法公式。

答案： 1. 解：
(1)${S}_{1}=(a+b)(a-b)$，${S}_{2}={a}^{2}-{b}^{2}$。
(2)$(a+b)(a-b)={a}^{2}-{b}^{2}$。

2. 下列可以运用平方差公式计算的有①④(填序号)。
① $ (a + b)(-b + a) $；② $ (-a + b)(a - b) $；
③ $ (a + b)(-a - b) $；④ $ (a - b)(-a - b) $。

答案： 2. ①④

3. 计算 $ a^{2} - (a + 1)(a - 1) $ 的结果是(A)

A.$ 1 $
B.$ -1 $
C.$ 2a^{2} + 1 $
D.$ 2a^{2} - 1 $

答案： 3. A

4. 计算：
(1) $ (5 - 2a)(5 + 2a) $。
(2) $ (xy + 5)(xy - 5) $。
(3) $ (\frac{1}{3}x + 4)(-\frac{1}{3}x + 4) $。
(4) $ (-4a + 3)(-4a - 3) $。
(5) $ x(x + 2) + (1 + x)(1 - x) $。
(6) $ (x + 3)(x - 3)(x^{2} + 9) $。

答案： 4. 解：
(1)原式$={5}^{2}-{(2a)}^{2}=25-4{a}^{2}$。
(2)原式$={(xy)}^{2}-{5}^{2}={x}^{2}{y}^{2}-25$。
(3)原式$={4}^{2}-{\left(\dfrac{1}{3}x\right)}^{2}=16-\dfrac{1}{9}{x}^{2}$。
(4)原式$={(-4a)}^{2}-{3}^{2}=16{a}^{2}-9$。
(5)原式$={x}^{2}+2x+1-{x}^{2}=2x+1$。
(6)原式$=({x}^{2}-9)({x}^{2}+9)={x}^{4}-81$。

5. （教材 P114 新增练习 T3 变式）运用平方差公式进行简便计算：
(1) $ 10\frac{1}{5}×9\frac{4}{5} $。
(2) $ 1007×993 $。

答案： 5. 解：
(1)原式$=\left(10+\dfrac{1}{5}\right)× \left(10-\dfrac{1}{5}\right)={10}^{2}-{\left(\dfrac{1}{5}\right)}^{2}=99\dfrac{24}{25}$。
(2)原式$=(1000+7)× (1000-7)={1000}^{2}-{7}^{2}=999951$。