第81页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
9. 化简:$x(x - 3)-(2x - 1)(x + 2)$。
答案:
原式=x²-3x-(2x²+4x-x-2)=x²-3x-(2x²+3x-2)=x²-3x-2x²-3x+2=-x²-6x+2.
10. 若关于$x$的多项式$(2x^{2}+ax)(x - 1)$展开合并后不含$x^{2}$项,则$a$的值是()
A.$2$
B.$\frac{1}{2}$
C.$0$
D.$-2$
A.$2$
B.$\frac{1}{2}$
C.$0$
D.$-2$
答案:
A
11. 观察下列两个多项式相乘的运算过程:
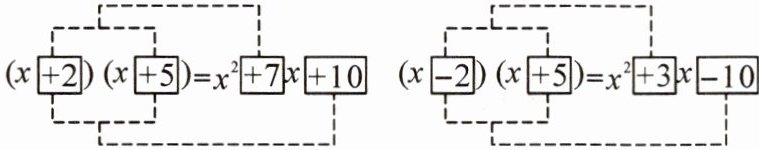
根据你发现的规律,若$(x + a)(x + b)=x^{2}-7x + 12$,则$a$,$b$的值可能分别是()
A.$-3$,$-4$
B.$-3$,$4$
C.$3$,$-4$
D.$3$,$4$
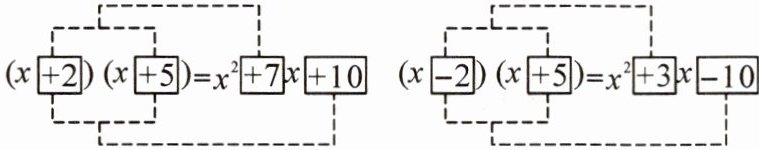
根据你发现的规律,若$(x + a)(x + b)=x^{2}-7x + 12$,则$a$,$b$的值可能分别是()
A.$-3$,$-4$
B.$-3$,$4$
C.$3$,$-4$
D.$3$,$4$
答案:
A
12. 有足够多张如图所示的A类、B类正方形卡片和C类长方形卡片。若要拼一个长为$3a + 2b$,宽为$a + b$的大长方形,则需要C类卡片的张数为()
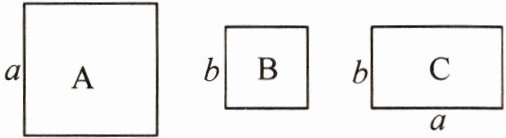
A.$3$
B.$4$
C.$5$
D.$6$
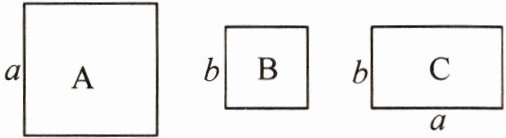
A.$3$
B.$4$
C.$5$
D.$6$
答案:
C
13. 设$M=(x - 3)(x - 7)$,$N=(x - 2)(x - 8)$,则$M$与$N$的大小关系为()
A.$M\lt N$
B.$M\gt N$
C.$M = N$
D.不能确定
A.$M\lt N$
B.$M\gt N$
C.$M = N$
D.不能确定
答案:
B
14. 已知$m + n = mn$,则$(m - 1)(n - 1)=\underline{\quad\quad}$。
答案:
1
15. 新考向 新定义问题 $4$个数$a$,$b$,$c$,$d$排列成$\begin{vmatrix}a&b\\c&d\end{vmatrix}$,我们称之为二阶行列式。规定它的运算法则为$\begin{vmatrix}a&b\\c&d\end{vmatrix}=ad - bc$。若$\begin{vmatrix}x - 2&x + 3\\x + 1&x - 2\end{vmatrix}=13$,则$x=\underline{\quad\quad}$。
答案:
-3/2
16. 华师二附中校本经典题 已知甲长方形相邻两边长相差$6$,乙长方形相邻两边长相差$2$,甲、乙两个长方形的周长相等。问:哪个长方形的面积更大?大多少?
答案:
设甲长方形相邻两边长分别为m,m+6,乙长方形相邻两边长分别为n,n+2.由题意,得2(m+m+6)=2(n+n+2),解得m=n-2.
∴甲长方形的面积为m(m+6)=(n-2)(n-2+6)=n²+2n-8,乙长方形的面积为n(n+2)=n²+2n.
∵n²+2n-(n²+2n-8)=8,
∴乙长方形的面积更大,大8.
∴甲长方形的面积为m(m+6)=(n-2)(n-2+6)=n²+2n-8,乙长方形的面积为n(n+2)=n²+2n.
∵n²+2n-(n²+2n-8)=8,
∴乙长方形的面积更大,大8.
17. 湖南师大附中校本经典题 你能化简$(x - 1)(x^{n - 1}+x^{n - 2}+\cdots+x + 1)$吗?遇到这样的复杂问题时,我们可以先从简单的情形入手,然后归纳出一些方法。
(1) 填空:
$(x - 1)(x + 1)=\underline{\quad\quad}$;
$(x - 1)(x^{2}+x + 1)=\underline{\quad\quad}$;
$(x - 1)(x^{3}+x^{2}+x + 1)=\underline{\quad\quad}$。
(2) 猜想:$(x - 1)(x^{n - 1}+x^{n - 2}+\cdots+x + 1)=\underline{\quad\quad}$。
(3) 请你利用上面的结论计算:
$2^{99}+2^{98}+\cdots+2 + 1$。
(1) 填空:
$(x - 1)(x + 1)=\underline{\quad\quad}$;
$(x - 1)(x^{2}+x + 1)=\underline{\quad\quad}$;
$(x - 1)(x^{3}+x^{2}+x + 1)=\underline{\quad\quad}$。
(2) 猜想:$(x - 1)(x^{n - 1}+x^{n - 2}+\cdots+x + 1)=\underline{\quad\quad}$。
(3) 请你利用上面的结论计算:
$2^{99}+2^{98}+\cdots+2 + 1$。
答案:
(1)(x-1)(x⁹⁹+x⁹⁸+…+x+1)=x¹⁰⁰-1
(2)2⁹⁹+2⁹⁸+…+2+1=(2-1)(2⁹⁹+2⁹⁸+…+2+1)=2¹⁰⁰-1
(1)(x-1)(x⁹⁹+x⁹⁸+…+x+1)=x¹⁰⁰-1
(2)2⁹⁹+2⁹⁸+…+2+1=(2-1)(2⁹⁹+2⁹⁸+…+2+1)=2¹⁰⁰-1
查看更多完整答案,请扫码查看


