第69页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
8. 如图,△ABC,△ADE 及△EFG 都是等边三角形,D,G 分别为 AC,AE 的中点. 若 AB=4,则图形 ABCDEFG 外围的周长是 (
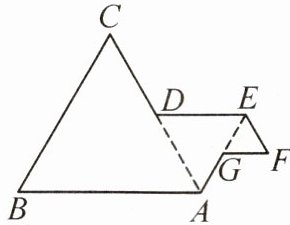
A.12
B.14
C.15
D.16
C
)
A.12
B.14
C.15
D.16
答案:
C
9. (2024·哈尔滨)如图,在△ABC 中,AB=AC,分别以点 A 和点 B 为圆心,大于 $\frac{1}{2}AB$ 的长为半径作弧,两弧相交于 M,N 两点,作直线 MN 交 BC 于点 D,连接 AD. 若∠B=50°,则∠DAC= (
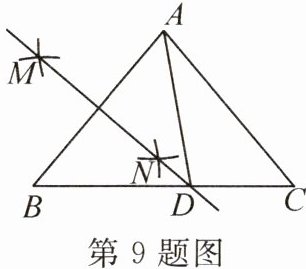
A.20°
B.50°
C.30°
D.80°
C
)
A.20°
B.50°
C.30°
D.80°
答案:
C
10. (2024·重庆)如图,在△ABC 中,AB=AC,∠A=36°,BD 平分∠ABC 交 AC 于点 D. 若 BC=2,则 AD 的长为

2
.
答案:
2
11. 如图,△ABC 是等边三角形,点 D,E,F 分别在 BC,AB,CA 的延长线上,且 BE=AF=CD. 求证:△DEF 是等边三角形.


答案:
证明:$\because \triangle ABC$是等边三角形,$\therefore \angle BAC=\angle ABC=\angle ACB=60^{\circ}$,$AB=AC=BC$.$\therefore \angle EAF=\angle EBD=120^{\circ}$.$\because BE=AF$,$BE+AB=AF+AC$,即$AE=CF$.$\because \triangle AFD≌\triangle BDE$(SAS),$\therefore EF=ED$同.理可得$\triangle AEF≌\triangle CFD$,$\therefore EF=FD$.$\therefore EF=ED=FD$.$\therefore \triangle DEF$为等边三角形.
12. (2023·泸州龙马潭区期末)如图,灯塔 C 在海岛 A 的北偏东 75°方向,某天上午 8 时整,一艘船从海岛 A 出发,以 15 海里/时的速度由西向东航行,10 时整到达 B 处,此时测得灯塔 C 在 B 处的北偏东 60°方向.
(1)求 B 处到灯塔 C 的距离.
(2)已知在以灯塔 C 为中心,周围 16 海里的范围内均有暗礁,若该船继续由西向东航行,是否有触礁的危险?请说明理由.
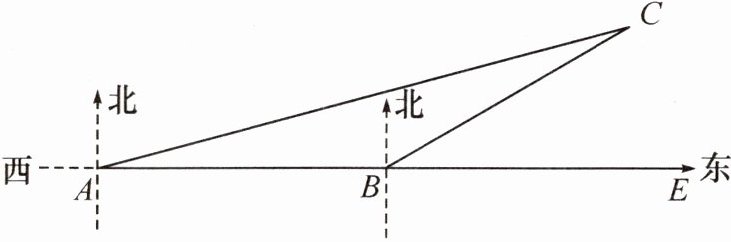
(1)求 B 处到灯塔 C 的距离.
(2)已知在以灯塔 C 为中心,周围 16 海里的范围内均有暗礁,若该船继续由西向东航行,是否有触礁的危险?请说明理由.

答案:
(1)解:根据题意,得$\angle BAC=90^{\circ}-75^{\circ}=15^{\circ}$,$\angle CBE=90^{\circ}-60^{\circ}=30^{\circ}$,$AB=15× (10-8)=30$(海里).$\because \angle ABC=15^{\circ}+30^{\circ}=45^{\circ}$,$\angle C=180^{\circ}-15^{\circ}-45^{\circ}=120^{\circ}$.由正弦定理得$\frac{BC}{\sin \angle BAC}=\frac{AB}{\sin \angle C}$,即$\frac{BC}{\sin 15^{\circ}}=\frac{30}{\sin 120^{\circ}}$,解得$BC=10\sqrt{6}-10\sqrt{2}\approx 10$(海里).
答:B处到灯塔C的距离为30海里.
(2)解:有触礁的危险.理由:过点C作$CD\perp AE$于点D.$\because \angle CBD=30^{\circ}$,$BC=30$海里,$\therefore CD=\frac{1}{2}BC=15$海里.$\because 15<16$,$\therefore$该船继续由西向东航行,会有触礁的危险.
(1)解:根据题意,得$\angle BAC=90^{\circ}-75^{\circ}=15^{\circ}$,$\angle CBE=90^{\circ}-60^{\circ}=30^{\circ}$,$AB=15× (10-8)=30$(海里).$\because \angle ABC=15^{\circ}+30^{\circ}=45^{\circ}$,$\angle C=180^{\circ}-15^{\circ}-45^{\circ}=120^{\circ}$.由正弦定理得$\frac{BC}{\sin \angle BAC}=\frac{AB}{\sin \angle C}$,即$\frac{BC}{\sin 15^{\circ}}=\frac{30}{\sin 120^{\circ}}$,解得$BC=10\sqrt{6}-10\sqrt{2}\approx 10$(海里).
答:B处到灯塔C的距离为30海里.
(2)解:有触礁的危险.理由:过点C作$CD\perp AE$于点D.$\because \angle CBD=30^{\circ}$,$BC=30$海里,$\therefore CD=\frac{1}{2}BC=15$海里.$\because 15<16$,$\therefore$该船继续由西向东航行,会有触礁的危险.
13. (2024·泸州泸县期中)如图,在等边三角形 ABC 中,AB=AC=10 cm. 点 M,N 都以 1 cm/s 的速度运动,点 M 在线段 CB 上由点 C 向点 B 运动,点 N 在线段 BA 上由点 B 向点 A 运动,两点同时出发. 当两点运动时间为 t s 时,△BMN 是直角三角形,则 t 的值为 (
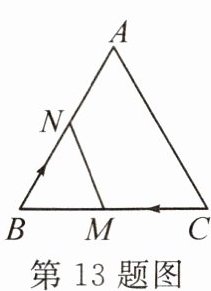
A.$\frac{10}{3}$
B.$\frac{20}{9}$
C.$\frac{10}{3}$ 或 $\frac{20}{3}$
D.$\frac{5}{3}$ 或 $\frac{10}{3}$
C
)
A.$\frac{10}{3}$
B.$\frac{20}{9}$
C.$\frac{10}{3}$ 或 $\frac{20}{3}$
D.$\frac{5}{3}$ 或 $\frac{10}{3}$
答案:
C
14. 如图,在△AB₁C₁ 中,AC₁ = B₁C₁,∠C₁ = 20°,在 B₁C₁ 上取一点 C₂,延长 AB₁ 到点 B₂,使得 B₁B₂ = B₁C₂;在 B₂C₂ 上取一点 C₃,延长 AB₂ 到点 B₃,使得 B₂B₃ = B₂C₃;在 B₃C₃ 上取一点 C₄,延长 AB₃ 到点 B₄,使得 B₃B₄ = B₃C₄……按此操作进行下去,那么第 n 个三角形的内角∠ABₙCₙ =
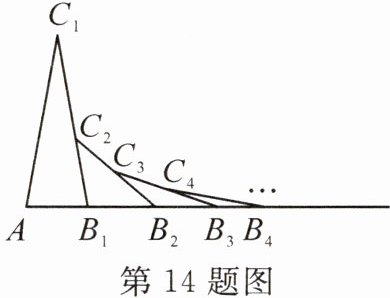
$\left(\frac{80}{2^{n-1}}\right)^{\circ}$
. (用含 n 的式子表示)
答案:
$\left(\frac{80}{2^{n-1}}\right)^{\circ}$
查看更多完整答案,请扫码查看


