《2025年名校课堂八年级数学上册人教版5四川专版》

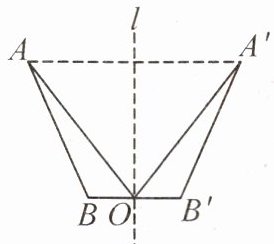
9. (教材 P65 新增练习 T3 变式)如图，线段 AB 与 A′B′关于直线 l 对称，BB′交直线 l 于点 O，连接 AO，A′O.
(1)AB=A'B'，OA=OA，直线 l 垂直平分线段BB'.
(2)△OAB 与△OA′B′关于直线 l成轴对称，△OAB≌△OA′B′，∠ABO=∠A'B'O，∠AOB′=∠A'OB.
(3)连接 AA′，试判断 AA′与 BB′的位置关系，并说明理由.

答案：
(1)A'B' OA BB'
(2)成轴对称 ≌ A'B'O A'OB
(3)AA' // BB' 理由:
∵AA'⊥l,BB'⊥l,
∴AA' // BB'.

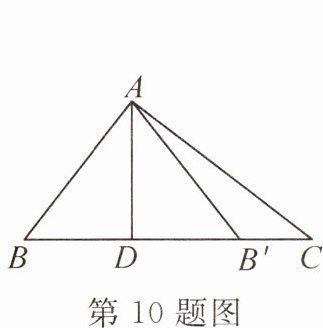
10. 如图，在 Rt△ACB 中，∠BAC=90°，AD⊥BC，垂足为 D，△ABD 与△AB′D 关于直线 AD 对称.若∠B′AC=14°，则∠B=(D)

A.38°
B.48°
C.50°
D.52°

答案： D

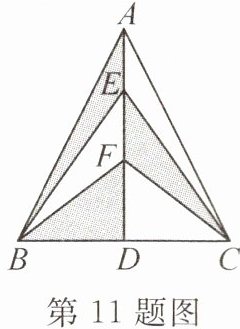
11. 如图，AD 所在直线是△ABC 的对称轴，E，F 是 AD 上的两点.若 BD=3，AD=6，则图中阴影部分的面积是12.

答案： 12

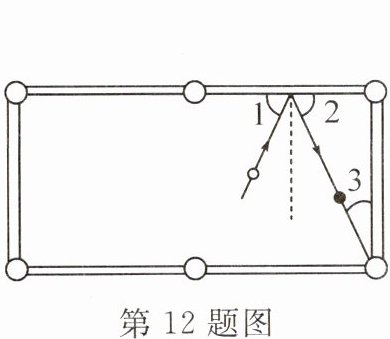
12. 如图，击打白球，使白球沿如图所示的路线撞击桌沿，反弹后将黑球撞入袋中.若∠3=25°，则∠1=65°.

答案： 65°

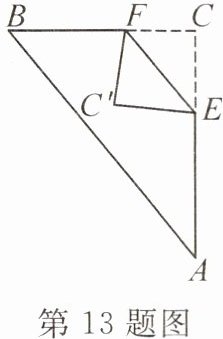
13. 如图，将直角三角形纸片 ABC 的直角 C 沿 EF 折叠，点 C 落到纸片内部的点 C′处.如果∠FEC′=40°，那么∠BFC′的度数为80°.

答案： 80°

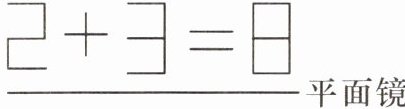
14. (1)一次晚会上，主持人出了一道题目：“如何把 2+3=8 变成一个真正的等式？”如图，小兰仅仅拿了一面镜子，就很快解决了这个问题.你知道她是怎么做的吗？
(2)请你编一道与(1)类似的题目.

答案：
(1)小兰的镜子起到了一个对称轴的作用.图略.
(2)答案不唯一,例如:如何把“5+1=3”变成真正的等式.

15. 如图，点 P 在∠AOB 的内部，点 C 和点 P 关于 OA 对称，点 P 和点 D 关于 OB 对称，连接 CD 交 OA 于点 M，交 OB 于点 N，连接 PM，PN.
(1)①若∠AOB=60°，求∠COD 的度数.
②若∠AOB=n°，则∠COD=2n°(用含 n 的代数式表示).
(2)若 CD=4，则△PMN 的周长为4.

答案：
(1)①点C和点P关于OA对称,点M在直线OA上,
∴△COM 与△POM关于直线OA对称.
∴∠AOC=∠AOP,同理可得,∠BOD= ∠BOP.
∴∠COD=∠AOC+∠AOP+∠BOP+∠BOD= 2∠AOP+2∠BOP=2(∠AOP+∠BOP)=2∠AOB=2×60°=120°;②2n°
(2)4