《2025年通城学典课时作业本七年级数学上册人教版南通专版》

12. (2024·海安期中)已知$a - b = 3$,$c + d = 2$,则$(b + c)-(a - d)$的值为-1.

答案： -1

13. 若多项式$4x^{2}-3x + 7与多项式5x^{3}+(m - 2)x^{2}-2x + 3$相减后,结果不含$x^{2}$项,则$m$的值为6.

答案： 6

14. (教材P101例8变式)先化简,再求值：
(1)$2(2x^{2}-\frac{1}{2}xy - y^{2})-(4x^{2}+4xy - 2y^{2})$,其中$x = 3$,$y = -1$；
(2)$4mn - [6(mn - m^{2})-4(2mn - m^{2})]$,其中$m = -3$,$n = \frac{1}{2}$.

答案：
(1) 原式$=-5xy$. 当$x = 3$，$y = -1$时，原式$=-5×3×(-1)=15$
(2) 原式$=6mn + 2m^{2}$. 当$m = -3$，$n=\frac{1}{2}$时，原式$=6×(-3)×\frac{1}{2} + 2×(-3)^{2}=9$

15. 甲、乙、丙三个车间加工一批零件,甲车间加工了$x$个,乙车间加工的比甲车间加工的2倍少35个,丙车间加工的比甲车间加工的一半多36个,这三个车间共加工了多少个零件？

答案： 解：乙车间加工的零件数为$2x - 35$个，丙车间加工的零件数为$\frac{1}{2}x + 36$个。
三个车间共加工零件数为：$x + (2x - 35) + (\frac{1}{2}x + 36)$
$=x + 2x - 35 + \frac{1}{2}x + 36$
$=(1 + 2 + \frac{1}{2})x + (-35 + 36)$
$=\frac{7}{2}x + 1$
答：这三个车间共加工了$(\frac{7}{2}x + 1)$个零件。

16. 有这样一道题：已知$A = 2a^{2}+2b^{2}-3c^{2}$,$B = 3a^{2}-b^{2}-2c^{2}$,$C = c^{2}+2a^{2}-3b^{2}$,当$a = 1$,$b = 2$,$c = 3$时,求$A - B + C$的值. 小刚说：“题目中给出的$b = 2$,$c = 3$是多余条件.”他的说法正确吗？为什么？

答案： 解：他的说法正确。
因为 $A - B + C = (2a^{2}+2b^{2}-3c^{2}) - (3a^{2}-b^{2}-2c^{2}) + (c^{2}+2a^{2}-3b^{2})$
$= 2a^{2}+2b^{2}-3c^{2} - 3a^{2}+b^{2}+2c^{2} + c^{2}+2a^{2}-3b^{2}$
$=(2a^{2}-3a^{2}+2a^{2}) + (2b^{2}+b^{2}-3b^{2}) + (-3c^{2}+2c^{2}+c^{2})$
$=a^{2}$
所以 $A - B + C$ 的化简结果为 $a^{2}$，其值与 $b$，$c$ 的取值无关。因此题目中给出的 $b = 2$，$c = 3$ 是多余条件。

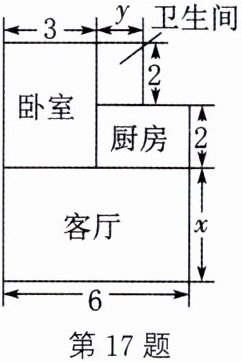
17. 小王购买了一套经济适用房,他准备在地面铺上地砖,房屋结构如图所示,根据图中的数据(单位：米),解答下面的问题：
(1)用含$x$,$y$的整式表示地面的总面积；
(2)若每平方米地砖的价格为200元,求铺地砖的总费用.

答案：
(1) 解：由图可知，地面总面积可看作大长方形面积减去右上角小长方形面积。大长方形长为6米，宽为$(x + 2 + 2)$米，面积为$6(x + 2 + 2)$平方米；右上角小长方形长为$(6 - 3 - y)$米，宽为2米，面积为$2(6 - 3 - y)$平方米。则地面总面积为：
$\begin{aligned}&6(x + 2 + 2)-2(6 - 3 - y)\\=&6(x + 4)-2(3 - y)\\=&6x + 24 - 6 + 2y\\=&6x + 2y + 18\end{aligned}$
答：地面的总面积为$(6x + 2y + 18)$平方米。
(2) 解：每平方米地砖价格为200元，总费用为总面积乘以单价，即：
$(6x + 2y + 18)×200 = 1200x + 400y + 3600$
答：铺地砖的总费用为$(1200x + 400y + 3600)$元。