《2025年通城学典课时作业本七年级数学上册人教版南通专版》

15. 宋代数学家杨辉称“幻方”为“纵横图”,传说最早出现的幻方是夏禹时代的“洛书”,杨辉的著作《续古摘奇算法》中总结了“洛书”的构造. 在如图所示的三阶幻方中,每行、每列、每条斜对角线上的三个数之和都相等,则“”位置上的数是(D)
A.$4$
B.$5$
C.$6$
D.$7$

答案： D

16. 已知关于$x的一元一次方程\frac{x}{2025} - a = 2025x的解是x = 5$,则关于$y的一元一次方程\frac{y + 2}{2025} - 2025y = a + 4050$的解是______$ y = 3 $.

答案： $ y = 3 $

17. (2024·通州期末)某商店采购了一批节能灯,每盏灯$20$元. 在运输过程中损坏了$2$盏,然后以每盏$25$元的价格售完,共获利$150$元. 该商店共采购了40盏节能灯.

答案： 40

18. 某公路一侧原有路灯$106$盏(公路两端均装有路灯),相邻两盏路灯之间的距离为$36$米. 为节约用电,现计划全部更换为新型节能灯,且相邻两盏路灯之间的距离变为$54$米,则需更换新型节能灯71盏.

答案： 71 解析：设需更换新型节能灯 $ x $ 盏，则 $ 54(x - 1) = 36×(106 - 1) $，解得 $ x = 71 $。所以需更换新型节能灯 71 盏。

19. 解方程:
(1) $3(x - 2) - 4(2x + 1) = 7$;
(2) $\frac{0.1x - 0.2}{0.02} - \frac{x + 1}{0.5} = 3$.

答案：
(1) $ x = -\frac{17}{5} $
(2) $ x = 5 $

20. 老师在批改小刚作业时发现,小刚在解方程$\frac{x + 1}{2} - 1 = ■ + \frac{2 - x}{3}$时,把“$2 - x$”抄成了“$x - 2$”,解得$x = 5$,而且“$■$”处的数也模糊不清了.
(1) 求“$■$”处的数;
(2) 请你求出原方程正确的解.

答案：
(1) 设“■”处的数为 $ a $。将 $ x = 5 $ 代入 $ \frac{x + 1}{2} - 1 = ■ + \frac{x - 2}{3} $，得 $ \frac{5 + 1}{2} - 1 = a + \frac{5 - 2}{3} $，解得 $ a = 1 $。所以“■”处的数为 1
(2) 因为“■”处的数为 1，所以原方程为 $ \frac{x + 1}{2} - 1 = 1 + \frac{2 - x}{3} $，解得 $ x = \frac{13}{5} $

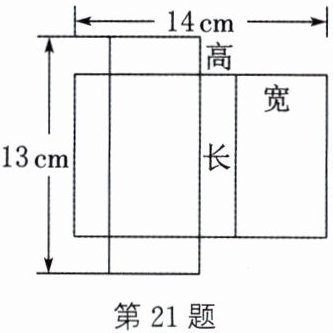
21. 某种长方体包装盒的表面展开图如图所示,如果该长方体包装盒的长比宽多$4cm$,求这种长方体包装盒的体积.

答案： 设这种长方体包装盒的宽为 $ x cm $，则它的高为 $ \frac{14}{2} - x = (7 - x) cm $，长为 $ (x + 4) cm $。由题意，得 $ (x + 4) + 2(7 - x) = 13 $，解得 $ x = 5 $，则 $ 7 - x = 2 $，$ x + 4 = 9 $。所以这种长方体包装盒的长为 9 cm，宽为 5 cm，高为 2 cm，则体积为 $ 9×5×2 = 90(cm^{3}) $