第52页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
15. (2024·南通)2024年5月,财政部下达1582亿元资金,支持地方进一步巩固和完善城乡统一、重在农村的义务教育经费保障机制.将“1582亿”用科学记数法表示为(
A.$158.2× 10^{9}$
B.$15.82× 10^{10}$
C.$1.582× 10^{11}$
D.$1.582× 10^{12}$
C
)A.$158.2× 10^{9}$
B.$15.82× 10^{10}$
C.$1.582× 10^{11}$
D.$1.582× 10^{12}$
答案:
C
16. 下列计算错误的是(
A.$- 3 - 5 = - 8$
B.$3÷ 9× \left( - \frac{1}{9}\right) = - 3$
C.$8÷ \left( - \frac{1}{4}\right) = - 32$
D.$3× 2^{3} = 24$
B
)A.$- 3 - 5 = - 8$
B.$3÷ 9× \left( - \frac{1}{9}\right) = - 3$
C.$8÷ \left( - \frac{1}{4}\right) = - 32$
D.$3× 2^{3} = 24$
答案:
B
17. 有理数$a$,$b$,$c$在数轴上对应点的位置如图所示,有下列结论:①$abc > 0$;②$b - a < 0$;③$a + c > 0$;④$\vert b - c\vert + \vert a - b\vert = \vert a - c\vert$.其中,正确的个数为(
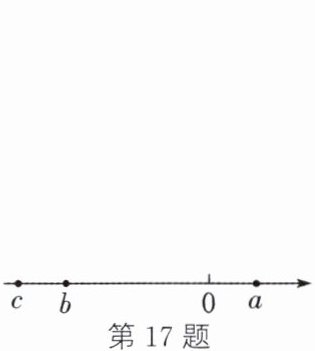
A.$1$
B.$2$
C.$3$
D.$4$
C
)
A.$1$
B.$2$
C.$3$
D.$4$
答案:
C
18. (新考法·新定义题)定义新运算“$*$”,规定$a*b = [(a + b)÷ (a - b)]^{3}$(其中$a\neq b$),例如$1*3 = [(1 + 3)÷ (1 - 3)]^{3} = [4÷ ( - 2)]^{3} = ( - 2)^{3} = - 8$,则$( - 9)*( - 15)$的值为(
A.$- 64$
B.$- 4$
C.$4$
D.$64$
A
)A.$- 64$
B.$- 4$
C.$4$
D.$64$
答案:
A
19. (新考向·传统文化)在如图所示的三阶幻方中,填写了一些数、式子和汉字(其中每个式子或汉字都表示一个数).若每一横行,每一竖列以及每条斜对角线上的3个数之和都相等,则“坚、持、不、懈”这四个字表示的数之和为(
A.$18$
B.$19$
C.$21$
D.$22$
D
)A.$18$
B.$19$
C.$21$
D.$22$
答案:
D 解析:根据题意,得 $2x + 2 - 18 = -10 + 0$,解得 $x = 3$,所以“持”表示的数是 $-18 + 0 - (-10) = -8$. 所以每一横行,每一竖列以及每条斜对角线上的 $3$ 个数之和为 $2x + 2 + 0 + (-8) = 2×3 + 2 - 8 = 0$. 所以“坚”表示的数是 $0 - (-8) - (-10) = 0 + 8 + 10 = 18$, “不”表示的数是 $0 - 0 - (x - 5) = -(3 - 5) = 2$, “懈”表示的数是 $0 - 0 - (-10) = 10$. 所以“坚、持、不、懈”这四个字表示的数之和为 $18 + (-8) + 2 + 10 = 22$.
20. 若数轴上点$A表示的数是-1$,点$B到点A的距离为2025$,则点$B$表示的数是
$2024$ 或 $-2026$
.
答案:
$2024$ 或 $-2026$
21. 若$\vert m - n\vert = n - m$,且$\vert m\vert = 4$,$\vert n\vert = 3$,则$(m + n)^{2} = $
49 或 1
.
答案:
$49$ 或 $1$
22. “五月天山雪,无花只有寒”,反映出地形对气温的影响.若海拔每升高100米,气温约下降$0.6{\hspace{0pt}}^{\circ }C$.有一座海拔为2750米的山,在这座山上海拔为250米的地方测得气温是$8{\hspace{0pt}}^{\circ }C$,则此时山顶的气温约为
-7
${\hspace{0pt}}^{\circ }C$.
答案:
$-7$
23. 已知$\vert a\vert = 2$,且$a < 1$,$b$,$c$互为倒数,则$a^{3} + 3 - 4bc$的值为
$-9$
.
答案:
$-9$
24. (2024·通州期中)在电子工程中,数字电路使用的是二进制系统,而采用八进制编码的数也经常用于显示屏控制、芯片编程和微处理器设备中.现用二进制记数法表示正整数,例如:$3 = 2 + 1 = 1× 2^{1} + 1× 2^{0}$(规定当$a\neq 0$时,$a^{0} = 1$),记作$3 = (11)_{2}$,$12 = 8 + 4 = 1× 2^{3} + 1× 2^{2} + 0× 2^{1} + 0× 2^{0}$,记作$12 = (1100)_{2}$.用八进制记数法表示正整数,例如:$83 = 64 + 16 + 3 = 1× 8^{2} + 2× 8^{1} + 3× 8^{0}$,记作$83 = (123)_{8}$,则将$(1011101)_{2}$转换成八进制数为______
135
.
答案:
$135$ 解析: $(1011101)_{2} = 1×2^{6} + 0×2^{5} + 1×2^{4} + 1×2^{3} + 1×2^{2} + 0×2^{1} + 1×2^{0} = 64 + 0 + 16 + 8 + 4 + 0 + 1 = 93$, 则 $93 = 64 + 24 + 5 = 1×8^{2} + 3×8^{1} + 5×8^{0}$, 所以将 $(1011101)_{2}$ 转换成八进制数为 $135$.
查看更多完整答案,请扫码查看


