第31页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
8. (数形结合思想)如图,数轴上A,B两点所表示的数分别为a,b,且$a+b>0,ab<0$,则原点的位置在 (
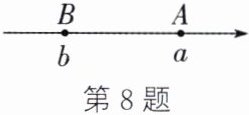
A.点A的右边
B.点B的左边
C.A,B两点之间,且靠近点A
D.A,B两点之间,且靠近点B
D
)
A.点A的右边
B.点B的左边
C.A,B两点之间,且靠近点A
D.A,B两点之间,且靠近点B
答案:
D
9. 从5,-3,2,-4中任取两个数相乘,所得的积最小是 (
A.-6
B.8
C.-15
D.-20
D
)A.-6
B.8
C.-15
D.-20
答案:
D
10. (分类讨论思想)(1)若$|a|= 8,|b|= 2$,且$a+b>0$,则$ab= $
(2)若$|x|= 4,|y|= 7$,且$x-y>0$,则$xy= $
16或-16
;(2)若$|x|= 4,|y|= 7$,且$x-y>0$,则$xy= $
28或-28
.
答案:
(1) 16或-16
(2) 28或-28
(1) 16或-16
(2) 28或-28
11. 有理数a,b,c,d在数轴上的对应点的位置如图所示,用“>”或“<”填空:

(1)$ab$
(2)$ac$
(3)$(a+b)(c+d)$
(4)$(d-a)(b-c)$

(1)$ab$
>
0;(2)$ac$
<
0;(3)$(a+b)(c+d)$
<
0;(4)$(d-a)(b-c)$
<
0.
答案:
(1) >
(2) <
(3) <
(4) <
(1) >
(2) <
(3) <
(4) <
12. 某数学小组的10名同学站成一列做报数游戏,规则:从前面第1名同学开始,每名同学依次报自己序号的倒数的2倍加1,第1名同学报$(\frac {2}{1}+1)$,第2名同学报$(\frac {2}{2}+1)$,第3名同学报$(\frac {2}{3}+1)$……这样得到的10个数的积为
13. 计算:
(1)$(-0.8)×(-\frac {7}{4})$
(2)$(-1\frac {3}{5})×(+3\frac {3}{4})$
(3)$(-4)×(-12)-(-5)×|-11|$
66
.13. 计算:
(1)$(-0.8)×(-\frac {7}{4})$
$\frac{7}{5}$
; (2)$(-1\frac {3}{5})×(+3\frac {3}{4})$
-6
;(3)$(-4)×(-12)-(-5)×|-11|$
103
.
答案:
12. 66 解析:第1名同学报的数是$\frac{2}{1}+1=\frac{3}{1}$,第2名同学报的数是$\frac{2}{2}+1=\frac{4}{2}$,第3名同学报的数是$\frac{2}{3}+1=\frac{5}{3}$,第4名同学报的数是$\frac{2}{4}+1=\frac{6}{4}$……第10名同学报的数是$\frac{2}{10}+1=\frac{12}{10}$,所以10个数的积为$\frac{3}{1}×\frac{4}{2}×\frac{5}{3}×\frac{6}{4}×…×\frac{12}{10}=\frac{11×12}{1×2}=66$。
13. 计算:
(1)$(-0.8)×(-\frac {7}{4})$;
(2)$(-1\frac {3}{5})×(+3\frac {3}{4})$;
(3)$(-4)×(-12)-(-5)×|-11|$.
(1)$(-0.8)×(-\frac {7}{4})$;
(2)$(-1\frac {3}{5})×(+3\frac {3}{4})$;
(3)$(-4)×(-12)-(-5)×|-11|$.
答案:
1. (1)
解:$(-0.8)×(-\frac{7}{4})=\frac{4}{5}×\frac{7}{4}=\frac{7}{5}$。
2. (2)
解:$(-1\frac{3}{5})×(+3\frac{3}{4})=(-\frac{8}{5})×(\frac{15}{4})=-6$。
3. (3)
解:$(-4)×(-12)-(-5)×|-11|$
先计算乘法和绝对值:
$(-4)×(-12)=48$,$|-11| = 11$,$(-5)×|-11|=-5×11=-55$。
再计算减法:
原式$=48-(-55)=48 + 55=103$。
综上,(1)的结果为$\frac{7}{5}$;(2)的结果为$-6$;(3)的结果为$103$。
解:$(-0.8)×(-\frac{7}{4})=\frac{4}{5}×\frac{7}{4}=\frac{7}{5}$。
2. (2)
解:$(-1\frac{3}{5})×(+3\frac{3}{4})=(-\frac{8}{5})×(\frac{15}{4})=-6$。
3. (3)
解:$(-4)×(-12)-(-5)×|-11|$
先计算乘法和绝对值:
$(-4)×(-12)=48$,$|-11| = 11$,$(-5)×|-11|=-5×11=-55$。
再计算减法:
原式$=48-(-55)=48 + 55=103$。
综上,(1)的结果为$\frac{7}{5}$;(2)的结果为$-6$;(3)的结果为$103$。
14. (新考法·新定义题)规定一种新运算“*”:$a*b= (a+2)×2-b$,例如:$3*5= (3+2)×2-5= 10-5= 5$. 根据运算规律解决问题.
(1)求$7*(-3)$的值;
(2)$7*(-3)与(-3)*7$的值相等吗?
(1)求$7*(-3)$的值;
(2)$7*(-3)与(-3)*7$的值相等吗?
答案:
(1) $7*(-3)=(7+2)×2-(-3)=21$
(2) 因为$(-3)*7=[(-3)+2]×2-7=-9$,所以$7*(-3)$与$(-3)*7$的值不相等
(1) $7*(-3)=(7+2)×2-(-3)=21$
(2) 因为$(-3)*7=[(-3)+2]×2-7=-9$,所以$7*(-3)$与$(-3)*7$的值不相等
查看更多完整答案,请扫码查看


