第27页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
11. (新考法·新定义义题)规定图形 $\begin{array}{r} a\\ b\end{array} c表示运算a-b+c$,图形$\begin{array}{r} x\\ y\end{array} \begin{array}{r} w\\ z\end{array} 表示运算x+z-y-w$,则$\begin{array}{r} 1\\ 2\end{array} 3+\begin{array}{r} 4\\ 7\end{array} \begin{array}{r} 5\\ 6\end{array} = $
$\begin{array}{r} a\\ b\end{array} c表示运算a-b+c$,图形$\begin{array}{r} x\\ y\end{array} \begin{array}{r} w\\ z\end{array} 表示运算x+z-y-w$,则$\begin{array}{r} 1\\ 2\end{array} 3+\begin{array}{r} 4\\ 7\end{array} \begin{array}{r} 5\\ 6\end{array} = $
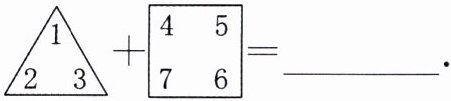
 $\begin{array}{r} a\\ b\end{array} c表示运算a-b+c$,图形$\begin{array}{r} x\\ y\end{array} \begin{array}{r} w\\ z\end{array} 表示运算x+z-y-w$,则$\begin{array}{r} 1\\ 2\end{array} 3+\begin{array}{r} 4\\ 7\end{array} \begin{array}{r} 5\\ 6\end{array} = $
$\begin{array}{r} a\\ b\end{array} c表示运算a-b+c$,图形$\begin{array}{r} x\\ y\end{array} \begin{array}{r} w\\ z\end{array} 表示运算x+z-y-w$,则$\begin{array}{r} 1\\ 2\end{array} 3+\begin{array}{r} 4\\ 7\end{array} \begin{array}{r} 5\\ 6\end{array} = $0
.
答案:
0 解析:根据题意,得 $1 - 2 + 3 + (4 + 6 - 7 - 5) = 0$.
12. 计算:
(1)$-41+38-59+72$;
(2)$-22\frac {2}{3}+14\frac {1}{4}-(-\frac {2}{3})-(+1.25)$;
(3)$(-1\frac {1}{2})-1\frac {1}{4}+(-2\frac {1}{2})-(-3\frac {3}{4})-|-1\frac {1}{4}|+\frac {1}{4}$.
(1)$-41+38-59+72$;
(2)$-22\frac {2}{3}+14\frac {1}{4}-(-\frac {2}{3})-(+1.25)$;
(3)$(-1\frac {1}{2})-1\frac {1}{4}+(-2\frac {1}{2})-(-3\frac {3}{4})-|-1\frac {1}{4}|+\frac {1}{4}$.
答案:
1. (1)
利用加法交换律和结合律$a + b + c + d=(a + c)+(b + d)$,则$-41 + 38-59 + 72=(-41-59)+(38 + 72)$。
先计算括号内的值:$-41-59=-(41 + 59)=-100$,$38 + 72 = 110$。
再计算$-100 + 110=10$。
2. (2)
先将小数化为分数,$1.25=\frac{5}{4}$,则$-22\frac{2}{3}+14\frac{1}{4}-(-\frac{2}{3})-(+1.25)=-22\frac{2}{3}+14\frac{1}{4}+\frac{2}{3}-\frac{5}{4}$。
利用加法交换律和结合律$a + b + c + d=(a + c)+(b + d)$,$(-22\frac{2}{3}+\frac{2}{3})+(14\frac{1}{4}-\frac{5}{4})$。
计算$-22\frac{2}{3}+\frac{2}{3}=-(22\frac{2}{3}-\frac{2}{3})=-22$,$14\frac{1}{4}-\frac{5}{4}=\frac{57}{4}-\frac{5}{4}=\frac{57 - 5}{4}=\frac{52}{4}=13$。
最后$-22 + 13=-9$。
3. (3)
先将带分数化为假分数,$-1\frac{1}{2}=-\frac{3}{2}$,$1\frac{1}{4}=\frac{5}{4}$,$-2\frac{1}{2}=-\frac{5}{2}$,$3\frac{3}{4}=\frac{15}{4}$,$\vert-1\frac{1}{4}\vert=\frac{5}{4}$。
则$(-1\frac{1}{2})-1\frac{1}{4}+(-2\frac{1}{2})-(-3\frac{3}{4})-\vert-1\frac{1}{4}\vert+\frac{1}{4}=(-\frac{3}{2})-\frac{5}{4}+(-\frac{5}{2})+\frac{15}{4}-\frac{5}{4}+\frac{1}{4}$。
利用加法交换律和结合律$(-\frac{3}{2}-\frac{5}{2})+(-\frac{5}{4}+\frac{15}{4}-\frac{5}{4}+\frac{1}{4})$。
计算$-\frac{3}{2}-\frac{5}{2}=-\frac{3 + 5}{2}=-4$,$-\frac{5}{4}+\frac{15}{4}-\frac{5}{4}+\frac{1}{4}=\frac{-5 + 15-5 + 1}{4}=\frac{6}{4}=\frac{3}{2}$。
最后$-4+\frac{3}{2}=-\frac{8}{2}+\frac{3}{2}=-\frac{5}{2}=-2\frac{1}{2}$。
综上,(1)的结果是$10$;(2)的结果是$-9$;(3)的结果是$-2\frac{1}{2}$。
利用加法交换律和结合律$a + b + c + d=(a + c)+(b + d)$,则$-41 + 38-59 + 72=(-41-59)+(38 + 72)$。
先计算括号内的值:$-41-59=-(41 + 59)=-100$,$38 + 72 = 110$。
再计算$-100 + 110=10$。
2. (2)
先将小数化为分数,$1.25=\frac{5}{4}$,则$-22\frac{2}{3}+14\frac{1}{4}-(-\frac{2}{3})-(+1.25)=-22\frac{2}{3}+14\frac{1}{4}+\frac{2}{3}-\frac{5}{4}$。
利用加法交换律和结合律$a + b + c + d=(a + c)+(b + d)$,$(-22\frac{2}{3}+\frac{2}{3})+(14\frac{1}{4}-\frac{5}{4})$。
计算$-22\frac{2}{3}+\frac{2}{3}=-(22\frac{2}{3}-\frac{2}{3})=-22$,$14\frac{1}{4}-\frac{5}{4}=\frac{57}{4}-\frac{5}{4}=\frac{57 - 5}{4}=\frac{52}{4}=13$。
最后$-22 + 13=-9$。
3. (3)
先将带分数化为假分数,$-1\frac{1}{2}=-\frac{3}{2}$,$1\frac{1}{4}=\frac{5}{4}$,$-2\frac{1}{2}=-\frac{5}{2}$,$3\frac{3}{4}=\frac{15}{4}$,$\vert-1\frac{1}{4}\vert=\frac{5}{4}$。
则$(-1\frac{1}{2})-1\frac{1}{4}+(-2\frac{1}{2})-(-3\frac{3}{4})-\vert-1\frac{1}{4}\vert+\frac{1}{4}=(-\frac{3}{2})-\frac{5}{4}+(-\frac{5}{2})+\frac{15}{4}-\frac{5}{4}+\frac{1}{4}$。
利用加法交换律和结合律$(-\frac{3}{2}-\frac{5}{2})+(-\frac{5}{4}+\frac{15}{4}-\frac{5}{4}+\frac{1}{4})$。
计算$-\frac{3}{2}-\frac{5}{2}=-\frac{3 + 5}{2}=-4$,$-\frac{5}{4}+\frac{15}{4}-\frac{5}{4}+\frac{1}{4}=\frac{-5 + 15-5 + 1}{4}=\frac{6}{4}=\frac{3}{2}$。
最后$-4+\frac{3}{2}=-\frac{8}{2}+\frac{3}{2}=-\frac{5}{2}=-2\frac{1}{2}$。
综上,(1)的结果是$10$;(2)的结果是$-9$;(3)的结果是$-2\frac{1}{2}$。
13. 一名足球守门员练习折返跑,从球门的位置出发,向前记作正数,返回记作负数,他的记录(单位:m)如下:$+5,-3,+10,-8,-6,+12,-10$.
(1)守门员是否回到了原来的位置?
(2)守门员离开球门的位置最远是多少?
(3)守门员一共跑了多少米?
(1)守门员是否回到了原来的位置?
(2)守门员离开球门的位置最远是多少?
(3)守门员一共跑了多少米?
答案:
(1) $5 - 3 + 10 - 8 - 6 + 12 - 10 = 0(\text{m})$,所以守门员回到了原来的位置
(2) 守门员离开球门的位置最远是 $12\ \text{m}$
(3) $| + 5 | + | - 3 | + | + 10 | + | - 8 | + | - 6 | + | + 12 | + | - 10 | = 54(\text{m})$,所以守门员一共跑了 $54\ \text{m}$
(1) $5 - 3 + 10 - 8 - 6 + 12 - 10 = 0(\text{m})$,所以守门员回到了原来的位置
(2) 守门员离开球门的位置最远是 $12\ \text{m}$
(3) $| + 5 | + | - 3 | + | + 10 | + | - 8 | + | - 6 | + | + 12 | + | - 10 | = 54(\text{m})$,所以守门员一共跑了 $54\ \text{m}$
14. (新情境·游戏活动)小彬和小丽玩一个抽卡片的游戏,游戏规则如下:每人每次抽取4张卡片,如果抽到白色卡片,那么加上卡片上的数;如果抽到阴影卡片,那么减去卡片上的数(初始值均为0).比较两人抽取的4张卡片的计算结果,结果大的为胜者.小彬抽到了如图①所示的4张卡片,小丽抽到了如图②所示的4张卡片,最后获胜的是谁?


答案:
小彬:$0 - (-\frac{1}{2}) + (-\frac{3}{2}) - (-5) + 4 = 8$, 小丽: $0 + (-\frac{1}{3}) - (-\frac{7}{6}) - 0 + 5 = 5\frac{5}{6}$. 因为 $8 > 5\frac{5}{6}$, 所以最后获胜的是小彬
查看更多完整答案,请扫码查看


