《2025年通城学典全程测评卷七年级数学上册苏科版》

12. (2024·常州金坛期中)有理数a,b,c,d在数轴上对应点的位置如图所示,这四个数中,绝对值最小的是c.

答案： c 解析:根据绝对值的定义,离原点的距离最近的数的绝对值最小,在这四个数中,有理数c在数轴上对应点的位置离原点最近,所以绝对值最小的数是c.

13. (2024·常州期中)已知a,b互为相反数,c是绝对值最小的数,d是负整数中最大的数,则$a+b+c+d=$-1.

答案： -1 解析:因为a,b互为相反数,所以$a + b = 0$.因为绝对值最小的数是0,所以c = 0.因为负整数中最大的数是-1,所以d = -1.所以$a + b + c + d = 0 + 0 + (-1) = -1$.

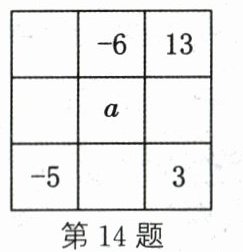
14. 新考法 探究题 幻方起源于我国,古人称之为纵横图.在如图所示的幻方中,各行、各列及各条对角线上的三个数之和均相等,则图中a的值为______.

4

答案： 4 解析:观察题图可知,a - 6 = 3 - 5,解得a = 4.

15. (2024·常州武进期中)按如图所示的程序进行计算,如果输入的数是72,那么最后输出的结果是288.

答案： 288 解析:当输入的数是72时,$72×|-\frac{1}{2}| = 72×\frac{1}{2} = 36$,$36÷[-(\frac{1}{2})^2] = 36÷(-\frac{1}{4}) = -144$.因为$-144 ＜ 100$,所以把-144作为输入的数再进行一次计算.当输入的数是-144时,$-144×|-\frac{1}{2}| = -144×\frac{1}{2} = -72$,$-72÷[-(\frac{1}{2})^2] = -72÷(-\frac{1}{4}) = 288$.因为$288 ＞ 100$,所以最后输出的结果是288.

16. 如图所示的图形是由小正方形按一定规律组成的,其中第1个图形中共有14个小正方形；第2个图形中共有19个小正方形；第3个图形中共有24个小正方形……第20个图形中小正方形的总个数为______.

109

答案： 109 解析:由题图可知,第1个图形中小正方形的总个数为$14 = 1×5 + 9$;第2个图形中小正方形的总个数为$19 = 2×5 + 9$;第3个图形中小正方形的总个数为$24 = 3×5 + 9\cdots\cdots$所以第n个图形中小正方形的总个数为$5n + 9$.当n = 20时,$5n + 9 = 5×20 + 9 = 109$,所以第20个图形中小正方形的总个数为109.

17. (6分)如图,把下列各数填入相应的圈内：$+13,-3.25,-\frac{3}{4},0,+\frac{12}{5},0.32,-\frac{1}{2}$.

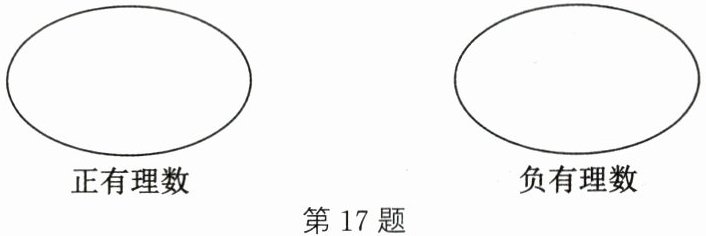
答案：
如图所示

18. (6分)(2024·盐城建湖期中)在如图所示的数轴上画出表示下列各数的点：4,0,$-(-1.5)$,$-1^{2024}$,-2.5,并用“＜”将这些数按从小到大的顺序连接起来.

答案：
在数轴上表示如图所示
$-2.5 ＜ -1^{2024} ＜ 0 ＜ -(-1.5) ＜ 4$