《2025年通城学典全程测评卷七年级数学上册苏科版》

1.(2024·扬州邗江期中)小明的身份证号码是320483200402126654,则小明的生日是 (B)
A.4月2日
B.2月12日
C.12月6日
D.4月21日

答案： B 解析:因为身份证号码的第11,12位是出生的月份,第13,14位是出生的日期,所以小明的生日是2月12日.

2.(2024·徐州新沂期中)下列各组数中互为相反数的一组是 (A)
A.-(-25)与$-5^2$
B.-3与-|-3|

C.(-3)^2$与$3^2$$
$D.(-2)^3$与$-2^3$

答案： A 解析:A.-(-25)=25,-5²=-25,因为-(-25)与-5²互为相反数,所以选项A符合题意.B.-|-3|=-3,所以选项B不符合题意.C.因为(-3)²=9,3²=9,所以(-3)²=3².所以选项C不符合题意.D.因为(-2)³=-8,-2³=-8,所以(-2)³=-2³.所以选项D不符合题意.

根据表中记录,你认为这次比赛小杰应该选 (B)
A.1号乒乓球
B.2号乒乓球
C.3号乒乓球
D.6号乒乓球

答案： B 解析:|+0.03|=0.03,|-0.02|=0.02,|+0.05|=0.05,|-0.03|=0.03,|-0.05|=0.05,|+0.04|=0.04,0.05=0.05＞0.04＞0.03=0.03＞0.02.因为绝对值越小越接近标准质量.所以最接近标准质量的是2号乒乓球.

4.(2024·无锡惠山期中)下列去括号正确的是 (B)
$A. a^2-(2a-b^2)= a^2-2a-b^2$
$B. -a^3+(-4a^2+1-3a)= -a^3-4a^2+1-3a$
$C. 2x^2-3(x-5)= 2x^2-3x+5$
$D. -(2x+y)+(-x^2+y^2)= -2x-y-x^2-y^2$

答案： B 解析:A.a²-(2a-b²)=a²-2a+b²≠a²-2a-b²,故选项A错误;B.-a³+(-4a²+1-3a)=-a³-4a²+1-3a,故选项B正确;C.2x²-3(x-5)=2x²-3x+15≠2x²-3x+5,故选项C错误;D.-(2x+y)+(-x²+y²)=-2x-y-x²+y²≠-2x-y-x²-y²,故选项D错误.

5.(2024·扬州邗江期中)如果|a|= 2,|b|= 5,a-b＞0,那么a-b的值是 (C)
A.-1
B.-3或-7
C.3或7
D.7

答案： C 解析:因为|a|=2,|b|=5,所以a=±2,b=±5.因为a-b＞0,所以a＞b.所以a=2,b=-5或a=-2,b=-5.当a=2,b=-5时,a-b=2-(-5)=7;当a=-2,b=-5时,a-b=-2-(-5)=3.综上所述,a-b的值是3或7.

6. 有下列说法:① -a一定是负数;② |-a|一定是正数;③ 倒数等于它本身的数是±1;④ 绝对值等于它本身的数是1;⑤ 平方等于它本身的数是1.其中,正确的个数是 (A)
A.1
B.2
C.3
D.4

答案： A 解析:①-a可能是负数、零、正数,故①说法错误,不符合题意;②|-a|一定是非负数,故②说法错误,不符合题意;③倒数等于它本身的数是±1,故③说法正确,符合题意;④绝对值等于它本身的数是非负数,故④说法错误,不符合题意;⑤平方等于它本身的数是0或1,故⑤说法错误,不符合题意.

7. 新情境 游戏活动 同学们都熟悉"幻方"游戏,现将"幻方"游戏稍作改进变成"幻圆"游戏.将-4,8,-12,16,-20,24,-28,32分别填入如图所示的圆圈内,使横、竖以及内外两个正方形顶点处圆圈内的4个数之和都相等,则m+n的值为 ( )

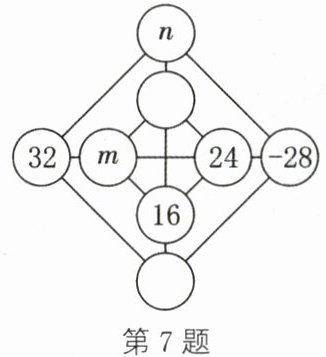
A.-12或-24
B.-4或-16
C.4或-4
D.4或-32

答案：
A 解析:因为-4+8-12+16-20+24-28+32=16,所以32+m+24+(-28)=8.所以m=-20.如图,设空白圆圈内的两个数分别为a,b,所以24+16+(-20)+a=8,解得a=-12.因为n+(-12)+16+b=8,所以n+b=4.所以n=-4或n=8.当n=-4时,b=8,此时m+n=-20-4=-24;当n=8时,b=-4,此时m+n=-20+8=-12.综上所述,m+n的值为-12或-24.
　　　　　　

8. 如图①所示的小长方形两条边的长分别为1,m(m＞1),现将这样5个大小形状完全相同的小长方形不重叠地放入如图②所示的大长方形中,图中未被覆盖部分用涂色表示,其面积分别为$S_1,S_2.$设面积为$S_1$的长方形一条边为x.若无论x为何值,图中涂色部分$S_1-S_2$的值总保持不变,此时$S_1-S_2$的值为 ( )

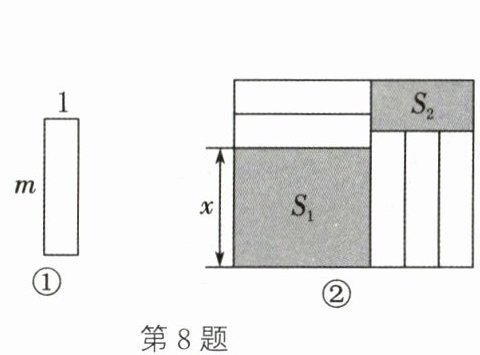
A.3/2
B.2
C.5/2
D.3

答案：
D 解析:如图,由题意,得AB=m+3,BC=x+2,所以S₁-S₂=xm-3(x+2-m)=xm-3x-6+3m=(m-3)x-6+3m.又因为涂色部分S₁-S₂的值总保持不变,所以m-3=0,解得m=3.所以S₁-S₂=-6+3×3=3.