《2025年通城学典全程测评卷七年级数学上册苏科版》

7. 如图,若图中各行、各列及对角线上的三个数之和都相等,则a= ______.

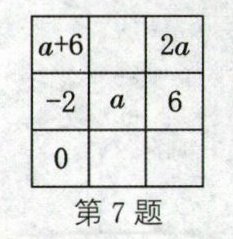
2

答案： 2 解析:根据题意,得-2+a+6=2a+a+0,解得a=2.

8. (2024·泰州靖江期末)如图,B,C两点把线段AD分成三部分,AB:BC:CD= 3:8:5,M为AD的中点.若CM= 15,则AD= ______.

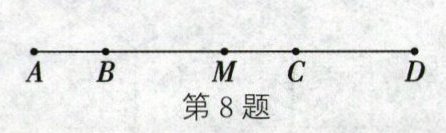
80

答案： 80 解析:因为AB:BC:CD=3:8:5,所以设AB=3x,BC=8x,CD=5x.所以AD=AB+BC+CD=3x+8x+5x=16x.因为M为AD的中点,所以AM=MD=1/2AD=8x.所以CM=MD-CD=8x-5x=3x.又因为CM=15,所以3x=15,解得x=5,则AD=16x=16×5=80.

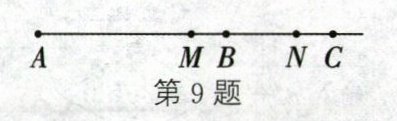
9. 如图,AB= 20 cm,C是线段AB延长线上一点,M为线段AC的中点,在线段BC上存在一点N(点N在点M的右侧且不与点B,C重合),使得6MN-NB= 60 cm,BN= kCN,则k的值为______1.5.

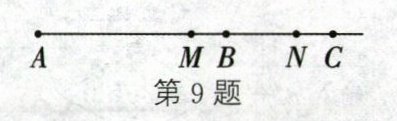
答案： 1.5 解析:设CN=2x cm,显然x＞0,所以BN=kCN=2kx cm.所以BC=BN+CN=(2kx+2x)cm.因为AB=20 cm,所以AC=AB+BC=(20+2kx+2x)cm.因为M为线段AC的中点,所以CM=1/2AC=(10+kx+x)cm.所以MN=CM-CN=(10+kx+x)-2x=(10+kx-x)cm.因为6MN-NB=60 cm,所以6(10+kx-x)-2kx=60.整理得(4k-6)x=0.因为x＞0,所以4k-6=0,解得k=1.5.

10. 将相同的长方形卡片按如图所示的方式摆放在一个直角上,每张长方形卡片的长为3,宽为2,以此类推,当摆放第2025张长方形卡片时,实线部分的长为______7089.

答案： 7089 解析:第1幅图实线部分的长为5,第2幅图实线部分的长为5+3=8,第3幅图实线部分的长为5+2+2+3=12,第4幅图实线部分的长为5+2+3+2+3=15,第5幅图实线部分的长为5+2+3+2+3+2+2=19,…,可以发现奇数项的规律为a₂ₘ₋₁=5+(m-1)×7(m为正整数,表示奇数项的项数位置,2m-1为奇数项的项数).因为2025属于奇数项,令2m-1=2025,所以m=1013.把m=1013代入a₂ₘ₋₁=5+(m-1)×7,可得a₂₀₂₅=5+(1013-1)×7=7089.综上所述,当摆放第2025张长方形卡片时,实线部分的长为7089.

11. (12分)请你根据妈妈和小明的对话内容(如图),列方程解决问题.已知妈妈每分钟步行60米,小明每分钟骑行240米,则小明能在妈妈到达火车站前追上她吗？如果能,何时追上？

答案： 设小明需要x分钟才能追上妈妈.从7:30到7:45经过15分钟,根据题意,得60(15+x)=240x,解得x=5,所以240x=240×5=1200.因为1200＜1800,7时45分+5分=7时50分,所以小明能在妈妈到达火车站前追上她,7:50追上

12. (12分)某店铺老板到手机配件专卖店进货,该店推出关于甲、乙两种配件的促销活动,已知甲配件每件标价20元,乙配件每件标价4元,现有以下两个促销方案,方案一：买一送一(每买一件甲配件,送一件乙配件)；方案二：全场九折(即全部配件按标价的九折销售).
(1)若购买50件甲配件与200件乙配件,则两个方案所需的费用相差多少元？
(2)若购买甲配件的件数比乙配件少100时,两个方案所需的费用相同,则此时购买两种配件各多少件？

答案： （1）选择方案一所需费用为20×50+4×(200-50)=1600(元),选择方案二所需费用为(20×50+4×200)×0.9=1620(元).因为1620-1600=20(元),所以两个方案所需的费用相差20元 （2）设购买x件甲配件,则购买(x+100)件乙配件.根据题意,得20x+4(x+100-x)=0.9[20x+4(x+100)],解得x=25.所以x+100=25+100=125.所以此时购买25件甲配件,125件乙配件