《2025年通城学典全程测评卷七年级数学上册苏科版》

10. 如图,将一副三角板重叠放在一起,∠AOB= 90°,∠COD= 60°,∠AOB与∠COD的顶点重合于点O.若∠COB= 18°,则∠AOD的度数为132°.

答案： 132 解析:因为∠COB=18°,∠COD=60°,所以∠BOD=60° - 18°=42°.因为∠AOB=90°,所以∠AOD=90°+42°=132°.

11. 新情境 现实生活 有下列三个日常现象:① 用两根钉子就可以把一根木条固定在墙上;② 把弯曲的公路改直,就能够缩短路程;③ 体育课上,老师测量某个同学的跳远成绩.其中,可以用"两点之间,线段最短"来解释的现象是______②(填序号).

答案： ② 解析:① 用两根钉子就可以把一根木条固定在墙上,依据的是两点确定一条直线;② 把弯曲的公路改直,就能够缩短路程,依据的是两点之间线段最短;③ 体育课上,老师测量某个同学的跳远成绩,依据的是垂线段最短.

12. 已知点C在线段AB上,若AC= 10 cm,BC= 8 cm,D是AC的中点,则BD的长为13cm.

答案： 13 解析:如图,因为AC=10 cm,D是AC的中点,所以CD=$\frac{1}{2}$AC=$\frac{1}{2}$×10=5(cm).因为BC=8 cm,所以BD=CD+BC=5+8=13(cm).

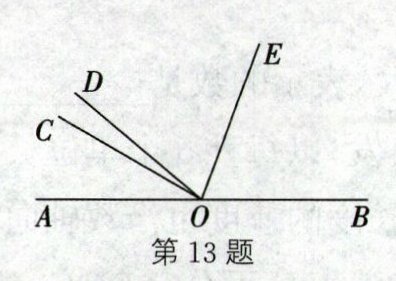
13. 如图,点A,O,B在同一条直线上,∠AOC= 3∠COD,OE平分∠BOD,若∠COD= 10°,则∠COE的度数为80°.

答案： 80 解析:因为∠AOC=3∠COD,∠COD=10°,所以∠AOC=3×10°=30°.所以∠AOD=∠AOC+∠COD=30°+10°=40°.因为∠AOD+∠BOD=180°,所以∠BOD=180° - ∠AOD=180° - 40°=140°.又因为OE平分∠BOD,所以∠DOE=$\frac{1}{2}$∠BOD=$\frac{1}{2}$×140°=70°.所以∠COE=∠DOE+∠COD=70°+10°=80°.

14. 一个平面内3条直线最多可以将这个平面分成7个区域.

答案： 7 解析:如图,当3条直线两两相交时,最多将这个平面分成7个区域.

15. 如图,在长方形ABCD中,E,F分别是AD,BC上的点,将长方形ABCD沿EF所在直线折叠,使点C,D分别落在点C',D'处,C'D'交BC边于点G.若∠DEF= 69°,则∠C'GF的度数为______°.


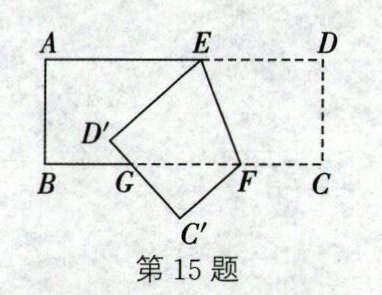
48

答案： 48 解析:因为长方形ABCD沿EF所在直线折叠,使点C,D分别落在点C',D'处,所以∠CFE=∠C'FE,∠C'=∠C.因为四边形ABCD为长方形,所以AD//BC,∠C=90°.所以∠GFE=∠DEF=69°.所以∠CFE=180° - ∠GFE=180° - 69°=111°.所以∠C'FE=111°.因为∠C'FE=∠C'FG+∠GFE,所以∠C'FG=∠C'FE - ∠GFE=111° - 69°=42°.在△GFC'中,∠C'GF=180° - ∠C' - ∠C'FG=180° - 90° - 42°=48°.

16. (2024·盐城期末)如图,直线MN分别与直线AB,CD相交于点E,F,EG平分∠MEB,交直线CD于点G.若∠MFD= ∠MEB= 66°,射线GP⊥EG于点G,则∠PGF= ______.

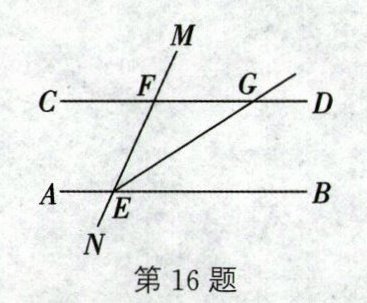
57°或123°

答案： 57°或123° 解析:因为∠MFD=∠MEB=66°,所以CD//AB.所以∠GEB=∠FGE.因为EG平分∠MEB,所以∠GEB=$\frac{1}{2}$∠MEB=33°.所以∠FGE=33°.分两种情况讨论,如图:① 当射线GP⊥EG于点G时,∠PGE=90°,∠PGF=∠PGE - ∠FGE=90° - 33°=57°;② 当射线GP'⊥EG于点G时,∠P'GE=90°,∠P'GF=∠P'GE+∠FGE=90°+33°=123°.综上所述,∠PGF的度数为57°或123°.

17. (8分)
(1) 把15°48'36"用度表示;
(2) 计算:33°16'28"+24°46'37".

答案： （1）因为36''=($\frac{1}{60}$)'×36=0.6',48'+0.6'=48.6',48.6'=($\frac{1}{60}$)°×48.6=0.81°,所以15°48'36''=15.81°. （2）33°16'28''+24°46'37''=57°62'65''=58°3'5''