《2025年通城学典全程测评卷七年级数学上册苏科版》

7. 按如图所示的运算程序,两次分别输入5和$\frac{1}{3}$,则两次输出的结果的积为15.

答案： 15 解析:分别输入5和$\frac{1}{3}$计算,输入5,得$x^{2}-3x = 10$,因为10 ＞ 0,所以输出5.输入$\frac{1}{3}$,得$x^{2}-3x = (\frac{1}{3})^{2}-3×\frac{1}{3}=-\frac{8}{9}$,因为$-\frac{8}{9}$ ＜ 0,所以输出3.所以5×3 = 15.

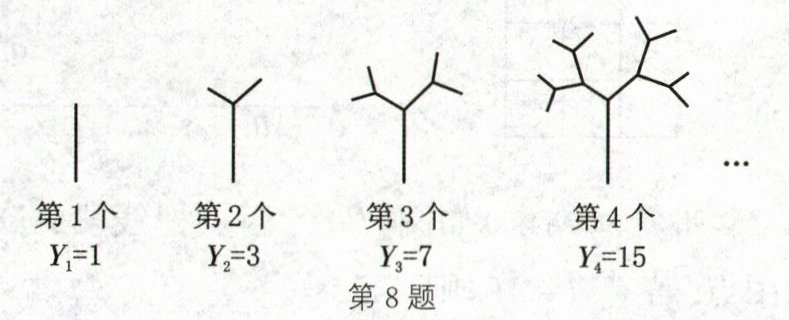
8. 如图,观察树枝分叉的规律图,若第n个图的树枝根数用$Y_n$表示,则$Y_6-Y_5$的值是______.


32

答案： 32 解析:由题图可知,Y₁ = 2¹ - 1 = 1,Y₂ = 2² - 1 = 3,Y₃ = 2³ - 1 = 7,Y₄ = 2⁴ - 1 = 15,…,Yₙ = 2ⁿ - 1,所以Y₆ - Y₅ = 2⁶ - 1 - (2⁵ - 1) = 32.

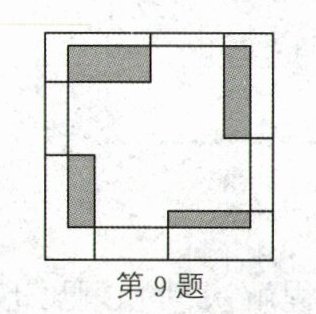
9. 如图,大正方形内有四个形状大小完全相同的长方形,且每个长方形的两条边分别在大正方形的边上,大正方形内有个小正方形与四个长方形有重叠(涂色部分).若两个正方形的周长分别为40和32,且四个涂色部分的周长和为44,则一个长方形的周长为______.

15

答案： 15 解析:如图,小正方形的周长减去涂色部分周长的一半等于4个长方形之间的长,即4个AB的长,即32 - 44×$\frac{1}{2}$ = 32 - 22 = 10,所以AB = 10÷4 = 2.5.因为长方形的长为DA,宽为BC,所以DA + BC = DC - AB.因为DC = 40÷4 = 10,所以一个长方形的周长 = (DA + BC)×2 = (DC - AB)×2 = (10 - 2.5)×2 = 15.

10. (2024·镇江期中)如图,王阿姨有块长方形空地ABCD,她打算用篱笆把空地四周围起来,为了划分出不同的种植区,在空地上用篱笆围了三个正方形,即正方形AEFG,正方形MNRH,正方形CPQN,其中点E在AB上,点M,N在BC上.若AE= 8米,MN= 6米,CN= 4米,她打算把茄子种在图中右上角涂色部分区域里,辣椒种在左下角涂色部分区域里,则茄子种植区与辣椒种植区所用篱笆的长度差为______米.

12

答案： 12 解析:因为四边形ABCD是长方形,所以设AB = DC = a米,AD = BC = b米.因为四边形AEFG是正方形,且AE = 8米,所以AE = EF = FG = AG = 8米.因为四边形MNRH是正方形,且MN = 6米,所以MN = NR = RH = HM = 6米.因为四边形CPQN是正方形,且CN = 4米,所以CP = PQ = QN = CN = 4米.所以BE = AB - AE = (a - 8)米,BM = BC - MN - CN = b - 6 - 4 = (b - 10)米,DG = AD - AG = (b - 8)米,PD = CD - CP = (a - 4)米,则茄子种植区所用篱笆的长度为2(DG + DP) = 2(b - 8 + a - 4) = (2a + 2b - 24)米,辣椒种植区所用篱笆的长度为2(BM + BE) = 2(b - 10 + a - 8) = (2a + 2b - 36)米.因为(2a + 2b - 24) - (2a + 2b - 36) = 12(米),所以茄子种植区与辣椒种植区所用篱笆的长度差为12米.

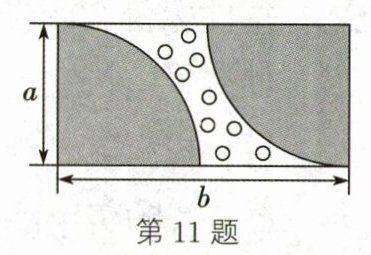
11. (15分)(2024·丹阳期中)如图,某校计划修建一座花坛,花坛呈长方形,两端四分之一圆铺设草地,中间空白区域铺设鹅卵石.
(1)用含a,b的代数式表示铺设鹅卵石的面积S；
(2)若a= 4米,b= 7米,每铺1平方米鹅卵石需180元,每铺1平方米草地需60元,修建该花坛共需花费多少元(π取3)？

答案：
(1)铺设鹅卵石的面积S = ab - $\frac{1}{4}$πa²×2 = ab - $\frac{1}{2}$πa²　
(2)当a = 4米,b = 7米,π≈3时,ab - $\frac{1}{2}$πa² = 4×7 - $\frac{1}{2}$×3×4² = 28 - 24 = 4(平方米),180×4 = 720(元).铺设草地的面积为$\frac{1}{2}$πa² = $\frac{1}{2}$×3×4² = 24(平方米),60×24 = 1440(元),720 + 1440 = 2160(元).所以修建该花坛共需花费2160元