《2025年名校课堂九年级数学上册人教版》

4. 如图，在 $ \triangle ABC $ 中，$ \angle ABC = 90^{\circ} $，以 $ AB $ 为直径作 $ \odot O $，交 $ AC $ 于点 $ D $，作切线 $ DE $ 交 $ BC $ 于点 $ F $.
(1) 求证：$ CF = DF $.
(2) 若 $ \angle BFD = 120^{\circ} $，$ DF = 1 $，求 $ AD $ 的长.

答案： 4.解：
(1)证明：连接OD.
∵∠ABC=90°，
∴∠A+∠C=90°.
∵DE为
⊙O的切线，
∴OD⊥DF.
∴∠FDO=90°.
∴∠FDC+∠ODA=
90°.
∵OD=OA，
∴∠ODA=∠A.
∴∠C=∠FDC.
∴CF=DF.
(2)连接BD.
∵∠BFD=120°，
∴∠CFD=60°.
∵CF=DF=1，
∴
△CDF为等边三角形.
∴CD=CF=1,∠C=60°.在Rt△BCD中，
BC=2CD=2.在Rt△ABC中，AC=2BC=4.
∴AD=AC-CD=4
-1=3.

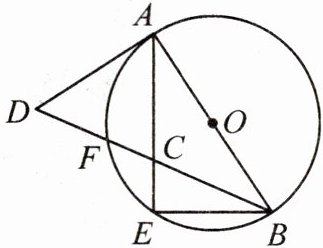
5. (2024·南充) 如图，在 $ \odot O $ 中，$ AB $ 是直径，$ AE $ 是弦，$ F $ 是 $ \overset{\frown}{AE} $ 上一点，$ \overset{\frown}{AF} = \overset{\frown}{BE} $，$ AE $，$ BF $ 相交于点 $ C $，$ D $ 为 $ BF $ 延长线上一点，且 $ \angle CAD = \angle CDA $.
(1) 求证：$ AD $ 是 $ \odot O $ 的切线.
(2) 若 $ BE = 4 $，$ AD = 2\sqrt{5} $，求 $ \odot O $ 的半径长.

答案： 5.解：
(1)证明：
∵AF=BE，
∴∠ABF=∠BAE.又
∵∠CAD+∠BAE
+∠CDA+∠ABF=180°，且∠CAD=∠CDA，
∴∠CAD+∠BAE
+∠CAD+∠BAE=180°.
∴∠OAD=∠CAD+∠BAE=90°.
AD⊥OA.又
∵OA是⊙O的半径，
∴AD是⊙O的切线.
(2)连接
AF.
∵AF=BE，BE=4，
∴AF=BE=4.
∵AB是⊙O的直径，
∴
∠AFB=90°.
∴∠AFD=90°.
∴DF=$\sqrt{AD^{2}-AF^{2}}$=
$\sqrt{(2\sqrt{5})^{2}-4^{2}}$=2.
∵∠BAD=∠AFB=90°，
∴AB$^{2}$=BD$^{2}$-AD$^{2}$
=AF$^{2}$+BF$^{2}$.设BF=x，则BD=2+x.
∴(2+x)$^{2}$-$(2\sqrt{5})^{2}$=4$^{2}$+
x$^{2}$，解得x=8.
∴BF=8.
∴AB=$\sqrt{AF^{2}+BF^{2}}$=$\sqrt{4^{2}+8^{2}}$=$4\sqrt{5}$.
∴⊙O的半径长为$2\sqrt{5}$.

6. 新考向 阅读理解 阅读以下材料，并完成相应的任务：

任务：
(1) 上述证明过程中的“依据 1”“依据 2”分别是指什么？
依据 1：圆的切线垂直于过切点的半径；
依据 2：直径所对的圆周角是直角.
(2) 请按照上面的证明思路，写出该证明的剩余部分.
(3) 已知图中 $ \odot O $ 的半径 $ 2 $，弦切角 $ \angle CAB = 30^{\circ} $，直接写出 $ AC $ 的长.

答案： 6.解：
(1)圆的切线垂直于过切点的半径直径所对的圆周角是直角
(2)
∵∠E=∠CAB.
∵AC=AC，
∴∠E=∠D.
∴∠CAB=∠D.
(3)
∵弦切角∠CAB=30°，由
(2)可知，∠CAB=∠D=30°.
∴∠E=
∠D=30°.
∵AE为⊙O的直径，
∴∠ACE=90°.在Rt△AEC中，
AE=2×2=4，
∴AC=$\frac{1}{2}$AE=2.