《2025年名校课堂九年级数学上册人教版》

1. (2024·甘南州)中国航天取得了举世瞩目的成就,为人类和平贡献了中国智慧和中国力量,下列是有关中国航天的图标,其文字上方的图案是中心对称图形的是 (D)

答案： 1.D

2. (2024·北京)下列图形中,既是轴对称图形又是中心对称图形的是 (B)

答案： 2.B

3. 如图,四边形 $ABCD$ 是菱形,$O$ 是两条对角线的交点,过点 $O$ 的三条直线将菱形分成阴影和空白部分. 若菱形的两条对角线的长分别为 $6$ 和 $8$,则阴影部分的面积为12.

答案： 3.12

4. 图 1、图 2 均为 $7×6$ 的正方形网格,点 $A,B,C$ 在格点上.
(1)在图 1 中确定格点 $D$,并画出以 $A,B,C,D$ 为顶点的四边形,使其为轴对称图形. (画一个即可)
(2)在图 2 中确定格点 $E$,并画出以 $A,B,C,E$ 为顶点的四边形,使其成为中心对称图形. (画一个即可)

答案： 1. （1）
解：根据轴对称图形的定义（如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形），我们可以这样确定$D$点：
先连接$BC$，作$BC$的垂直平分线，与网格线的交点可作为$D$点（答案不唯一）。例如，以$BC$为底边，作等腰三角形$BCD$（$BD = CD$），此时四边形$ABDC$是轴对称图形（对称轴为$BC$的垂直平分线）。
2. （2）
解：根据中心对称图形的定义（在平面内，把一个图形绕着某个点旋转$180^{\circ}$，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形）。
连接$AC$，取$AC$的中点$O$，延长$BO$到$E$，使$OE = BO$，则四边形$ABCE$是平行四边形（平行四边形是中心对称图形，绕着对角线交点旋转$180^{\circ}$与原图形重合）。
（1）答案不唯一，只要画出的四边形$ABCD$是轴对称图形即可；（2）答案不唯一，只要画出的四边形$ABCE$是中心对称图形即可。

5. 图 1 和图 2 中所有的小正方形都全等,将图 1 的正方形放在图 2 中①②③④的某一位置,使它与原来 $7$ 个小正方形组成的图形是中心对称图形,这个位置是 (C)

A.①
B.②
C.③
D.④

答案： 5.C

6. 如图,在矩形 $ABCD$ 中,$AB = 4$,$BC = 6$,$O$ 是矩形的对称中心,点 $E,F$ 分别在边 $AD,BC$ 上,连接 $OE,OF$. 若 $AE = BF = 2$,则 $OE + OF$ 的值为 (D)

A.$2\sqrt{2}$
B.$5\sqrt{2}$
C.$\sqrt{5}$
D.$2\sqrt{5}$

答案： 6.D

7. (教材 $P70$ 习题 $T8$ 变式)阅读材料:对于中心对称图形,过对称中心的任意一条直线都把这个图形分成全等的两部分,如图:

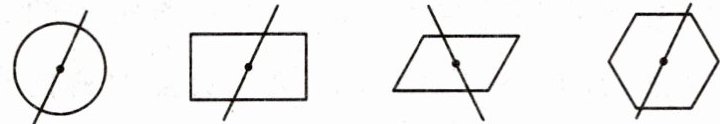
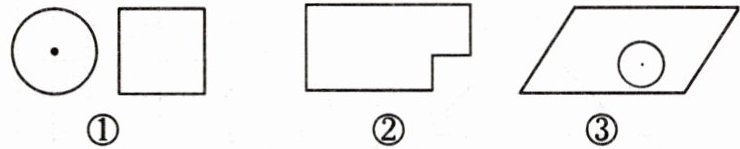
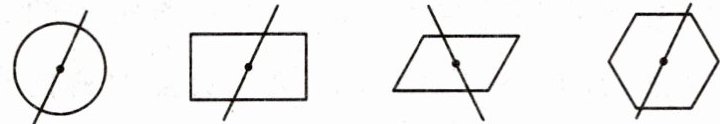
尝试应用:将下列各图分成面积相等的两部分. (不写作法,保留作图痕迹)

答案： 本题可根据中心对称图形的性质，通过找出对称中心，作直线将图形分成面积相等的两部分。
步骤一：分析图①
图①由一个圆和一个正方形组成，圆的对称中心是圆心，正方形的对称中心是两条对角线的交点。
连接圆心与正方形对角线交点的直线，即可将该图分成面积相等的两部分。
步骤二：分析图②
图②可看作是一个大长方形挖去一个小长方形。
分别找出大长方形和小长方形的对称中心（大长方形两条对角线交点，小长方形两条对角线交点），连接这两个对称中心的直线，能把该图分成面积相等的两部分。
步骤三：分析图③
图③由一个平行四边形和一个圆组成，平行四边形的对称中心是两条对角线的交点，圆的对称中心是圆心。
连接平行四边形对角线交点与圆心的直线，可将此图分成面积相等的两部分。
综上，按照上述方法分别对三个图形进行作图（由于无法直接作图，根据上述思路，通过找对称中心连线的方法即可完成分割） 。