第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
10. 如图,用一根$60\ cm$的铁丝制作一个“日”字形框架$ABCD$,铁丝恰好全部用完.设框架的宽$AB$为$x\ cm$.
(1)框架的长$AD$为
(2)矩形框架$ABCD$面积的最大值为

(1)框架的长$AD$为
\frac{1}{2}(60 - 3x)
$cm$(用含$x$的代数式表示).(2)矩形框架$ABCD$面积的最大值为
150
$cm^{2}$.
答案:
$10.(1)\frac{1}{2}(60 - 3x) (2)150$
11. 把边长为$20\ cm$的正方形硬纸板(如图1),在四个顶点处分别剪掉一个小正方形,折成一个无盖的长方体盒子(如图2),折纸厚度忽略不计,则折成的无盖盒子的侧面积(四个侧面的面积之和)最大是
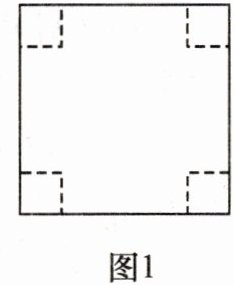
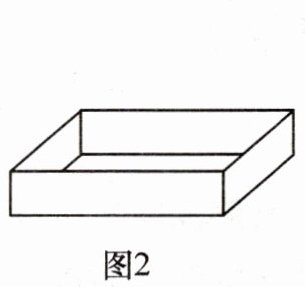
200
$cm^{2}$.

答案:
11.200
12. 为充分利用现有资源,学校“牧春园”计划用栅栏围出一块矩形花圃种植两种花卉.如图,矩形花圃$ABCD$一面靠墙(墙的长度为$12\ m$),另外三面用栅栏围成,中间再用栅栏$EF$把它分成两个面积相等的矩形.已知栅栏的总长度为$27\ m$,设$AB$的长为$x\ m$,矩形花圃$ABCD$的面积为$S\ m^{2}$.
(1)求$S$与$x$的函数关系式,并写出$x$的取值范围.
(2)当$AB$的长为多少时,矩形花圃$ABCD$的面积最大?最大面积是多少?

(1)求$S$与$x$的函数关系式,并写出$x$的取值范围.
(2)当$AB$的长为多少时,矩形花圃$ABCD$的面积最大?最大面积是多少?

答案:
12.解:$(1)S=x(27 - 3x)= -3x^{2}+27x,$$\because 0<27 - 3x\leqslant18,$$\therefore 5\leqslant x< 9.\therefore S= -3x^{2}+27x(5\leqslant x<9)。$$(2)S= -3x^{2}+27x= -3(x - \frac{9}{2})^{2}+\frac{243}{4},$$\because -3<0,$$5\leqslant x<9,$$\therefore $当 x=5 时,S 有最大值,最大
值为60。答:当 AB 的长为 5m 时,矩形花圃 ABCD 的面积最大,
最大面积是$60m^{2}。$
值为60。答:当 AB 的长为 5m 时,矩形花圃 ABCD 的面积最大,
最大面积是$60m^{2}。$
13. (本课时T7变式)两段互相垂直的墙$AB$和$AC$的长分别为$12\ m$和$3\ m$,用一段长为$23\ m$的篱笆围成一个矩形菜园(篱笆全部使用完),如图所示,矩形菜园的一边$AD$由墙$AC$和一节篱笆$CD$构成,一边$AF$靠在墙$AB$上,一边$EF$上有一扇$2\ m$宽的门.假设篱笆$CD$的长为$x\ m$,矩形菜园的面积为$S\ m^{2}(S>0)$,回答下面的问题:
(1)①用含$x$的式子表示篱笆$DE$的长为
②菜园的面积能不能等于$90\ m^{2}$?若能,求出此时$x$的值;若不能,请说明理由.
(2)求菜园面积的最大值.
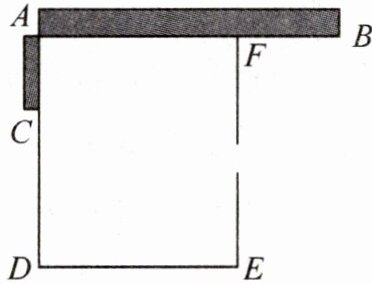
(1)①用含$x$的式子表示篱笆$DE$的长为
(22 - 2x)
$m$,$x$的取值范围是5\leqslant x<11
.②菜园的面积能不能等于$90\ m^{2}$?若能,求出此时$x$的值;若不能,请说明理由.
(2)求菜园面积的最大值.

答案:
13.解:$(1)①(22 - 2x) 5\leqslant x<11 ②$菜园的面积能等于$ 90m^{2}。$根
据题意,得(3 + x)(22 - 2x)=90,整理,得$x^{2}- 8x + 12=0。$解得$x_{1}$
=2,$x_{2}=6.\because 5\leqslant x<11,$$\therefore x=6。$(2)由题意,得 S=(3 + x)(22 -
$2x)= -2x^{2}+16x + 66= -2(x - 4)^{2}+98.\because -2$<0,
\therefore 当 x>4
时,S 随 x 的增大而减小。$\because 5\leqslant x<11,$$\therefore $当 x=5 时,S 有最大值,
最大值为$-2×(5 - 4)^{2}+98=96。$答:菜园面积的最大值为$96m^{2}。$
据题意,得(3 + x)(22 - 2x)=90,整理,得$x^{2}- 8x + 12=0。$解得$x_{1}$
=2,$x_{2}=6.\because 5\leqslant x<11,$$\therefore x=6。$(2)由题意,得 S=(3 + x)(22 -
$2x)= -2x^{2}+16x + 66= -2(x - 4)^{2}+98.\because -2$<0,
\therefore 当 x>4
时,S 随 x 的增大而减小。$\because 5\leqslant x<11,$$\therefore $当 x=5 时,S 有最大值,
最大值为$-2×(5 - 4)^{2}+98=96。$答:菜园面积的最大值为$96m^{2}。$
查看更多完整答案,请扫码查看


