第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. 新考向 真实情境 “卢沟晓月”是著名的北京八景之一,古时乾隆皇帝曾在秋日路过卢沟桥,赋诗“半钩留照三秋淡,一练分波平镜明”于此,并题“卢沟晓月”,立碑于桥头. 卢沟桥主桥拱可以近似看作抛物线,桥拱在水面的跨度 $ OA $ 约为 $ 22 $ 米,若按如图所示的方式建立平面直角坐标系,则主桥拱所在抛物线可以表示为 $ y = -\frac{13}{121}(x - 11)^2 + k $. 主桥拱最高点 $ P $ 与其在水中倒影 $ P' $ 之间的距离为(
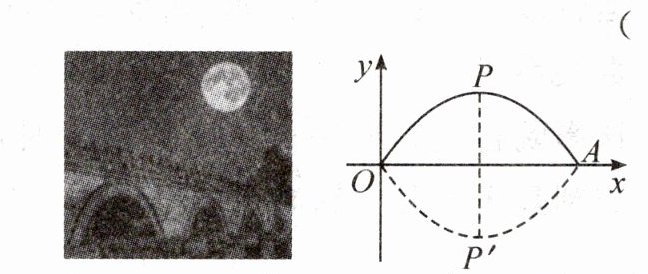
A.$ 11 $ 米
B.$ 13 $ 米
C.$ 22 $ 米
D.$ 26 $ 米
D
)
A.$ 11 $ 米
B.$ 13 $ 米
C.$ 22 $ 米
D.$ 26 $ 米
答案:
1.D
2. 如图所示,公路隧道的截面为抛物线形,线段 $ OA $ 表示水平的路面,以点 $ O $ 为坐标原点, $ OA $ 所在直线为 $ x $ 轴,以过点 $ O $ 垂直于 $ x $ 轴的直线为 $ y $ 轴,建立平面直角坐标系. 若 $ OA =$$10 \, m $,抛物线的顶点 $ P $ 到 $ OA $ 的距离为 $ 9 \, m $,则抛物线对应的函数解析式为
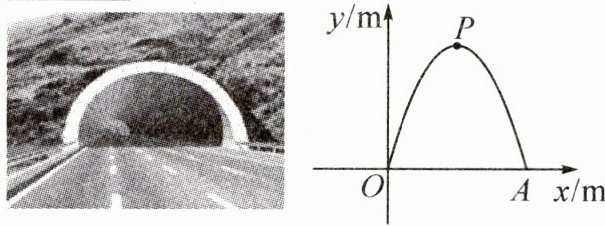
$y = - \frac { 9 } { 2 5 } ( x - 5 ) ^ { 2 } + 9$
.
答案:
2.$y = - \frac { 9 } { 2 5 } ( x - 5 ) ^ { 2 } + 9$
3. 某农户搭建有如图 1 所示的蔬菜大棚,其截面示意图如图 2 所示,其横截面塑料顶棚可以近似看作是抛物线,其中 $ OA $ 是地面所在的水平线,点 $ O $ 是塑料顶棚与地面的交点, $ AB $ 是保温墙,并且塑料顶棚最高点到点 $ O $ 的水平距离是 $ 6 $ 米,到地面 $ OA $ 的高度是 $ 3 $ 米. 现以 $ OA $ 所在直线为 $ x $ 轴,过点 $ O $ 垂直于 $ OA $ 的直线为 $ y $ 轴,建立平面直角坐标系. 若保温墙 $ AB $ 到点 $ O $ 的距离 $ OA = 8 $ 米,请你求出保温墙 $ AB $ 的高度.




答案:
3.解:设塑料顶棚所在抛物线的解析式为$y = a ( x - 6 ) ^ { 2 } + 3$.将点$O(0,0)$代入抛物线解析式,得$36a + 3 = 0$,解得$a = - \frac { 1 } { 1 2 }$.$\therefore$抛物线的解析式为$y = - \frac { 1 } { 1 2 } ( x - 6 ) ^ { 2 } + 3$.当$x = 8$时,$y = - \frac { 1 } { 1 2 } × ( 8 - 6 ) ^ { 2 } + 3 = \frac { 8 } { 3 }$.
答:保温墙$AB$的高度是$\frac { 8 } { 3 }$米.
答:保温墙$AB$的高度是$\frac { 8 } { 3 }$米.
4. 如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线. 若不考虑空气阻力,小球的飞行高度 $ h(m) $ 与飞行时间 $ t(s) $ 之间具有函数关系: $ h = -5t^2 + 20t $,则当小球飞行高度达到最高时,飞行时间 $ t = $

2
$ s $.
答案:
4.2
5. 新考向 真实情境 射水鱼(别名高射炮鱼)在水中看到水面上方的猎物 $ A $ (猎物的大小忽略不计)后,便向猎物射水,当猎物被水射中后射水鱼对其进行捕获. 如图,喷射出的水柱在空中呈抛物线形状,设喷出水柱的竖直高度为 $ y \, cm $ (水柱的竖直高度是指水柱与鱼嘴 $ B $ 所在水平面的距离),水柱与鱼嘴 $ B $ 的水平距离为 $ x \, cm $,建立如图所示的平面直角坐标系,得到如下数据:
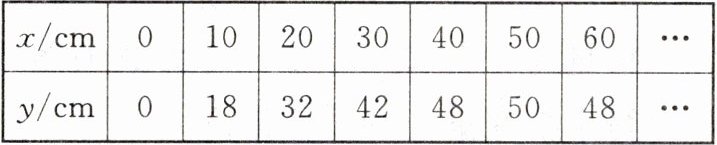
(1) 请结合表中所给数据,求此次射水过程中水柱轨迹所在抛物线的解析式.
(2) 若猎物 $ A $ 突然受到惊吓,退至点 $ (55, 45) $ 处,试判断该射水鱼此次射水喷出的水柱能否精准捕获猎物 $ A $,并说明理由.


(1) 请结合表中所给数据,求此次射水过程中水柱轨迹所在抛物线的解析式.
(2) 若猎物 $ A $ 突然受到惊吓,退至点 $ (55, 45) $ 处,试判断该射水鱼此次射水喷出的水柱能否精准捕获猎物 $ A $,并说明理由.

答案:
5.解:
(1)由表格数据可知,当$x = 40$和$x = 60$时,$y$的值相同,则该抛物线的对称轴为直线$x = \frac { 4 0 + 6 0 } { 2 } = 5 0$.$\because$当$x = 5 0$时,$y = 5 0$,$\therefore$设该抛物线的解析式为$y = a ( x - 5 0 ) ^ { 2 } + 5 0$.将$(0,0)$代入$y = a ( x - 5 0 ) ^ { 2 } + 5 0$,解得$a = - \frac { 1 } { 5 0 }$.$\therefore$此次射水过程中水柱轨迹所在抛物线的解析式为$y = - \frac { 1 } { 5 0 } ( x - 5 0 ) ^ { 2 } + 5 0$.
(2)不能.理由如下:当$x = 5 5$时,$y = - \frac { 1 } { 5 0 } ( x - 5 0 ) ^ { 2 } + 5 0 = 4 9 . 5 > 4 5$,$\therefore$该射水鱼此次射水喷出的水柱不能精准捕获到猎物$A$.
(1)由表格数据可知,当$x = 40$和$x = 60$时,$y$的值相同,则该抛物线的对称轴为直线$x = \frac { 4 0 + 6 0 } { 2 } = 5 0$.$\because$当$x = 5 0$时,$y = 5 0$,$\therefore$设该抛物线的解析式为$y = a ( x - 5 0 ) ^ { 2 } + 5 0$.将$(0,0)$代入$y = a ( x - 5 0 ) ^ { 2 } + 5 0$,解得$a = - \frac { 1 } { 5 0 }$.$\therefore$此次射水过程中水柱轨迹所在抛物线的解析式为$y = - \frac { 1 } { 5 0 } ( x - 5 0 ) ^ { 2 } + 5 0$.
(2)不能.理由如下:当$x = 5 5$时,$y = - \frac { 1 } { 5 0 } ( x - 5 0 ) ^ { 2 } + 5 0 = 4 9 . 5 > 4 5$,$\therefore$该射水鱼此次射水喷出的水柱不能精准捕获到猎物$A$.
查看更多完整答案,请扫码查看


