第91页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
12. 反证法是数学证明的一种重要方法.请将下面运用反证法进行证明的过程补全.
已知:在△ABC中,AB=AC.求证:∠B<90°.
证明:假设
∵AB=AC,
∴∠B=∠C≥90°.
∴∠A+∠B+∠C>180°.
这与
∴
∴∠B<90°.
已知:在△ABC中,AB=AC.求证:∠B<90°.
证明:假设
$\angle B\geq90°$
.∵AB=AC,
∴∠B=∠C≥90°.
∴∠A+∠B+∠C>180°.
这与
三角形内角和定理(或三角形的内角和等于$180°$)
相矛盾.∴
此假设
不成立.∴∠B<90°.
答案:
12.$\angle B\geq90°$ 三角形内角和定理(或三角形的内角和等于$180°$) 此假设
13. 已知点P不在⊙O上,且点P到⊙O上的点的最小距离是4cm,最大距离是9cm,则⊙O的直径是
$13\ cm$或$5\ cm$
.
答案:
13.$13\ cm$或$5\ cm$
14. 已知⊙O的半径为1,点P到圆心O的距离为d.若关于x的方程x²-2x+d=0没有实数根,则点P(
A.在⊙O的内部
B.在⊙O的外部
C.在⊙O上
D.在⊙O上或在⊙O的内部
B
)A.在⊙O的内部
B.在⊙O的外部
C.在⊙O上
D.在⊙O上或在⊙O的内部
答案:
14.B
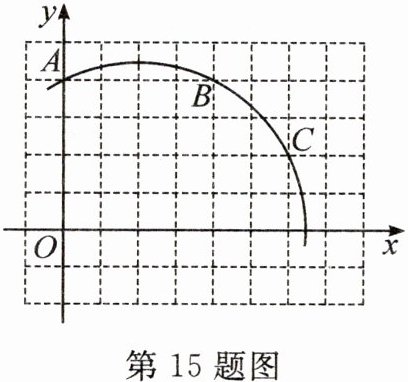
15. 如图,平面直角坐标系中,A(0,4),B(4,4),C(6,2),经过A,B,C三点的圆,圆心为M.若线段DM=4,则点D与⊙M的位置关系为(
A.点D在⊙M上
B.点D在⊙M外
C.点D在⊙M内
D.无法确定
C
)
A.点D在⊙M上
B.点D在⊙M外
C.点D在⊙M内
D.无法确定
答案:
15.C
16. 如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上(网格线的交点),用一个圆面去覆盖△ABC,则能够完全覆盖这个三角形的最小圆的半径是

$\sqrt{5}$
.
答案:
16.$\sqrt{5}$
17. 新考向 真实情境 “以铜为镜,可以正衣冠”.铜镜是我国古代人民勤劳和智慧的结晶.如图所示的是一个铜镜的残片,文物修复专家准备用现代高科技手段将其复原,使得“破镜重圆”.文物修复专家量得铜镜残片上最大的弦AB的长为16cm,铜镜上的点到弦AB的最大距离为6cm.
(1)请用尺规作图的方法,帮助文物修复专家找出铜镜所在圆的圆心(简要说明作图思路,不写具体作法,保留作图痕迹).
(2)请帮助文物修复专家求出铜镜所在圆的半径.

(1)请用尺规作图的方法,帮助文物修复专家找出铜镜所在圆的圆心(简要说明作图思路,不写具体作法,保留作图痕迹).
(2)请帮助文物修复专家求出铜镜所在圆的半径.

答案:
17.解:
(1)图略. 步骤:连接$AB$,作线段$AB$的垂直平分线$MN$交$AB$于点$C$,连接$AC$,作线段$AC$的垂直平分线$EF$,$EF$交$MN$于点$O$,点$O$即为所求.
(2)连接$OA$,设$AB$与$OC$交于点$D$.由题意,得$AB = 16\ cm$,$CD = 6\ cm$,则$AD = DB = 8\ cm$.设$\odot O$的半径为$r\ cm$,则$OD = (r - 6)\ cm$.在$Rt\triangle AOD$中,$AD^{2} + OD^{2} = AO^{2}$,即$8^{2} + (r - 6)^{2} = r^{2}$,解得$r = \frac{25}{3}$.$\therefore\odot O$的半径为$\frac{25}{3}\ cm$.
(1)图略. 步骤:连接$AB$,作线段$AB$的垂直平分线$MN$交$AB$于点$C$,连接$AC$,作线段$AC$的垂直平分线$EF$,$EF$交$MN$于点$O$,点$O$即为所求.
(2)连接$OA$,设$AB$与$OC$交于点$D$.由题意,得$AB = 16\ cm$,$CD = 6\ cm$,则$AD = DB = 8\ cm$.设$\odot O$的半径为$r\ cm$,则$OD = (r - 6)\ cm$.在$Rt\triangle AOD$中,$AD^{2} + OD^{2} = AO^{2}$,即$8^{2} + (r - 6)^{2} = r^{2}$,解得$r = \frac{25}{3}$.$\therefore\odot O$的半径为$\frac{25}{3}\ cm$.
18. 如图,点P(3,4),⊙P半径为2,A(2.8,0),B(5.6,0),点M是⊙P上的动点,点C是MB的中点,则AC的最小
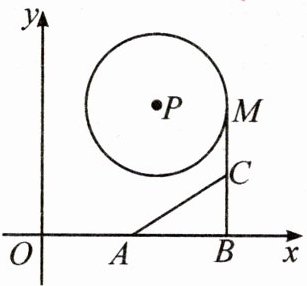
A.1.4
B.1.5
C.2.5
D.2.6
值
是(B
)
A.1.4
B.1.5
C.2.5
D.2.6
答案:
18.B
查看更多完整答案,请扫码查看


