《2025年名校课堂九年级数学上册人教版》

12. (2022·南充)如图，$AB$为$\odot O$的直径，弦$CD \perp AB$于点$E$，$OF \perp BC$于点$F$，$\angle BOF = 65^{\circ}$，则$\angle AOD =$(C)

A.$70^{\circ}$
B.$65^{\circ}$
C.$50^{\circ}$
D.$45^{\circ}$

答案： 12.C

13. 如图，$AB$是$\odot O$的直径，$\angle ACD = \angle CAB$，$AD = 2$，$AC = 4$，则$\odot O$的半径为$\sqrt{15}$.

答案： 13.$\sqrt{15}$

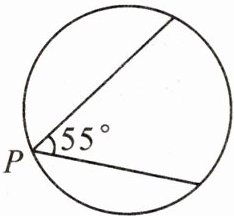
14. (2023·郴州)如图，某博览会上有一圆形展示区，在其圆形边缘的点$P$处安装了一台监视器，它的监控角度是$55^{\circ}$. 为了监控整个展示区，则最少需要在圆形边缘上共安装这样的监视器4台.

答案： 14.4

15. 新考向 真实情境 船在航行过程中，船长通常通过测定角度来确定是否会遇到暗礁，如图，$A$，$B$表示灯塔，暗礁分布在经过$A$，$B$两点的一个圆形区域内，$C$表示一个危险临界点，$\angle ACB$就是“危险角”，当船与两个灯塔的夹角大于“危险角”时，就有可能触礁；当船与两个灯塔的夹角小于“危险角”时，就能避免触礁.
(1)如图1，当船与两个灯塔的夹角$\alpha$大于“危险角”时，船位于哪个区域？为什么？
(2)如图2，当船与两个灯塔的夹角$\alpha$小于“危险角”时，船位于哪个区域？为什么？
]

答案： 15.解：
(1)当船与两个灯塔的夹角$\alpha$大于“危险角”时，船位于$\odot O$内.理由如下：延长$AP$交$\odot O$于点$F$，连接$BF.\because\angle C = \angle F$，$\angle APB ＞ \angle F$，$\therefore\angle APB ＞ \angle C$，即$\alpha ＞ \angle C.\therefore$当船与两个灯塔的夹角$\alpha$大于“危险角”时，船位于$\odot O$内.
(2)当船与两个灯塔的夹角$\alpha$小于“危险角”时，船位于$\odot O$外.理由如下：连接$BE.\because\angle AEB = \angle C$，$\angle AEB ＞ \angle P$，$\therefore\angle C ＞ \angle P$，即$\alpha ＜ \angle C.\therefore$当船与两个灯塔的夹角$\alpha$小于“危险角”时，船位于$\odot O$外.

1. (2024·苏州)如图，点$A$，$B$，$C$在$\odot O$上. 若$\angle OBC = 28^{\circ}$，则$\angle A =$62$^{\circ}$.

答案： 1.62

2. 如图，点$A$，$B$，$S$在圆上，若弦$AB$的长度等于圆半径长度的$\sqrt{2}$倍，则$\angle ASB$的度数是$45°$.

答案： 2.$45°$

3. 如图，在$\triangle ABC$中，$\angle ABC = 80^{\circ}$，$\angle A = 32^{\circ}$，点$B$，$C$在$\odot O$上，边$AB$，$AC$分别交$\odot O$于$D$，$E$两点，$B$是$\overset{\frown}{CBD}$的中点，则$\angle ABE =$$18°$.

答案： 3.$18°$

4. 如图，$AB$是$\odot O$的直径，弦$CD$交$AB$于点$E$，$\angle ACD = 55^{\circ}$，则$\angle BAD$的度数为(C)

A.$25^{\circ}$
B.$30^{\circ}$
C.$35^{\circ}$
D.$40^{\circ}$

答案： 4.C

5. 如图，$\odot P$经过平面直角坐标系的原点$O$，且分别交$x$轴、$y$轴于$A$，$B$两点，$C$为$\overset{\frown}{ACB}$的中点. 若$A(6,0)$，$AC = 5\sqrt{2}$，则点$B$的坐标是(0,8).

答案： 5.$(0,8)$