第69页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
10. (2024·安徽)如图,在由边长为1个单位长度的小正方形组成的网格中建立平面直角坐标系xOy,格点(网格线的交点)A,B,C,D的坐标分别为(7,8),(2,8),(10,4),(5,4)。
(1)以点D为旋转中心,将△ABC旋转180°得到△A₁B₁C₁,画出△A₁B₁C₁。
(2)直接写出以B,C₁,B₁,C为顶点的四边形的面积。
(3)在所给的网格图中确定一个格点E,使得射线AE平分∠BAC,写出点E的坐标。

(1)以点D为旋转中心,将△ABC旋转180°得到△A₁B₁C₁,画出△A₁B₁C₁。
(2)直接写出以B,C₁,B₁,C为顶点的四边形的面积。
(3)在所给的网格图中确定一个格点E,使得射线AE平分∠BAC,写出点E的坐标。

答案:
1. (1)
已知$A(7,8)$,$B(2,8)$,$C(10,4)$,$D(5,4)$。
根据旋转$180^{\circ}$的性质:点$(x,y)$绕点$(a,b)$旋转$180^{\circ}$后的对应点坐标为$(2a - x,2b - y)$。
对于点$A(7,8)$,绕$D(5,4)$旋转$180^{\circ}$,则$A_1$的横坐标$x_{A_1}=2×5 - 7 = 3$,纵坐标$y_{A_1}=2×4 - 8 = 0$,即$A_1(3,0)$;
对于点$B(2,8)$,绕$D(5,4)$旋转$180^{\circ}$,则$B_1$的横坐标$x_{B_1}=2×5 - 2 = 8$,纵坐标$y_{B_1}=2×4 - 8 = 0$,即$B_1(8,0)$;
对于点$C(10,4)$,绕$D(5,4)$旋转$180^{\circ}$,则$C_1$的横坐标$x_{C_1}=2×5 - 10 = 0$,纵坐标$y_{C_1}=2×4 - 4 = 4$,即$C_1(0,4)$。
然后连接$A_1B_1$,$B_1C_1$,$C_1A_1$,得到$\triangle A_1B_1C_1$。
2. (2)
由$B(2,8)$,$C_1(0,4)$,$B_1(8,0)$,$C(10,4)$。
我们可以利用平行四边形面积公式$S = 底×高$。
观察可得$BC_1// B_1C$,$BC_1=\sqrt{(2 - 0)^2+(8 - 4)^2}=\sqrt{4 + 16}=\sqrt{20}=2\sqrt{5}$,$B_1C=\sqrt{(10 - 8)^2+(4 - 0)^2}=\sqrt{4 + 16}=\sqrt{20}=2\sqrt{5}$,且$BC_1$与$B_1C$间的距离$h = 8 - 4=4$(也可利用割补法:$S=\frac{1}{2}×(8 - 2)×(8 - 4)+\frac{1}{2}×(10 - 0)×(8 - 4)=24$)。
以$B$,$C_1$,$B_1$,$C$为顶点的四边形是平行四边形,$S=(8 - 2)×(8 - 4)=24$。
3. (3)
利用角平分线的性质(角平分线上的点到角两边的距离相等)。
设$E(x,y)$,$AB$的长度$AB=\sqrt{(7 - 2)^2+(8 - 8)^2}=5$,$AC=\sqrt{(10 - 7)^2+(4 - 8)^2}=\sqrt{9 + 16}=5$,$\triangle ABC$是等腰三角形($AB = AC$)。
观察网格可得$E(10,8)$(可通过三角形全等或角平分线的判定(到角两边距离相等的点在角平分线上)来验证:$AB$所在直线$y = 8$,$AC$所在直线,先求$k_{AC}=\frac{8 - 4}{7 - 10}=-\frac{4}{3}$,$y-8=-\frac{4}{3}(x - 7)$,即$4x+3y=52$。点$E(10,8)$到$AB$($y = 8$)的距离$d_1 = 0$(在$AB$上),到$AC$:$4x + 3y-52 = 0$的距离$d_2=\frac{\vert4×10+3×8 - 52\vert}{\sqrt{4^2+3^2}}=0$(也可通过构造全等三角形,$\triangle ABE\cong\triangle ACE$($AB = AC$,$BE = CE$($E(10,8)$,$B(2,8)$,$C(10,4)$,$BE=\sqrt{(10 - 2)^2+(8 - 8)^2}=8$,$CE=\sqrt{(10 - 10)^2+(8 - 4)^2}=4$这种方法错误,重新用角平分线的判定:$AB$方向水平,$AC$:设$E(x,y)$,$AB$:$y = 8$,$AC$:$4x+3y - 52 = 0$,根据角平分线到两边距离相等$\vert y - 8\vert=\frac{\vert4x + 3y-52\vert}{5}$,结合网格可得$E(10,8)$)。
综上,(1)按上述坐标画出图形;(2)$24$;(3)$(10,8)$。
已知$A(7,8)$,$B(2,8)$,$C(10,4)$,$D(5,4)$。
根据旋转$180^{\circ}$的性质:点$(x,y)$绕点$(a,b)$旋转$180^{\circ}$后的对应点坐标为$(2a - x,2b - y)$。
对于点$A(7,8)$,绕$D(5,4)$旋转$180^{\circ}$,则$A_1$的横坐标$x_{A_1}=2×5 - 7 = 3$,纵坐标$y_{A_1}=2×4 - 8 = 0$,即$A_1(3,0)$;
对于点$B(2,8)$,绕$D(5,4)$旋转$180^{\circ}$,则$B_1$的横坐标$x_{B_1}=2×5 - 2 = 8$,纵坐标$y_{B_1}=2×4 - 8 = 0$,即$B_1(8,0)$;
对于点$C(10,4)$,绕$D(5,4)$旋转$180^{\circ}$,则$C_1$的横坐标$x_{C_1}=2×5 - 10 = 0$,纵坐标$y_{C_1}=2×4 - 4 = 4$,即$C_1(0,4)$。
然后连接$A_1B_1$,$B_1C_1$,$C_1A_1$,得到$\triangle A_1B_1C_1$。
2. (2)
由$B(2,8)$,$C_1(0,4)$,$B_1(8,0)$,$C(10,4)$。
我们可以利用平行四边形面积公式$S = 底×高$。
观察可得$BC_1// B_1C$,$BC_1=\sqrt{(2 - 0)^2+(8 - 4)^2}=\sqrt{4 + 16}=\sqrt{20}=2\sqrt{5}$,$B_1C=\sqrt{(10 - 8)^2+(4 - 0)^2}=\sqrt{4 + 16}=\sqrt{20}=2\sqrt{5}$,且$BC_1$与$B_1C$间的距离$h = 8 - 4=4$(也可利用割补法:$S=\frac{1}{2}×(8 - 2)×(8 - 4)+\frac{1}{2}×(10 - 0)×(8 - 4)=24$)。
以$B$,$C_1$,$B_1$,$C$为顶点的四边形是平行四边形,$S=(8 - 2)×(8 - 4)=24$。
3. (3)
利用角平分线的性质(角平分线上的点到角两边的距离相等)。
设$E(x,y)$,$AB$的长度$AB=\sqrt{(7 - 2)^2+(8 - 8)^2}=5$,$AC=\sqrt{(10 - 7)^2+(4 - 8)^2}=\sqrt{9 + 16}=5$,$\triangle ABC$是等腰三角形($AB = AC$)。
观察网格可得$E(10,8)$(可通过三角形全等或角平分线的判定(到角两边距离相等的点在角平分线上)来验证:$AB$所在直线$y = 8$,$AC$所在直线,先求$k_{AC}=\frac{8 - 4}{7 - 10}=-\frac{4}{3}$,$y-8=-\frac{4}{3}(x - 7)$,即$4x+3y=52$。点$E(10,8)$到$AB$($y = 8$)的距离$d_1 = 0$(在$AB$上),到$AC$:$4x + 3y-52 = 0$的距离$d_2=\frac{\vert4×10+3×8 - 52\vert}{\sqrt{4^2+3^2}}=0$(也可通过构造全等三角形,$\triangle ABE\cong\triangle ACE$($AB = AC$,$BE = CE$($E(10,8)$,$B(2,8)$,$C(10,4)$,$BE=\sqrt{(10 - 2)^2+(8 - 8)^2}=8$,$CE=\sqrt{(10 - 10)^2+(8 - 4)^2}=4$这种方法错误,重新用角平分线的判定:$AB$方向水平,$AC$:设$E(x,y)$,$AB$:$y = 8$,$AC$:$4x+3y - 52 = 0$,根据角平分线到两边距离相等$\vert y - 8\vert=\frac{\vert4x + 3y-52\vert}{5}$,结合网格可得$E(10,8)$)。
综上,(1)按上述坐标画出图形;(2)$24$;(3)$(10,8)$。
11. 如图,E是正方形ABCD的边CD上一点,把△ADE绕点A顺时针旋转90°得到△ABF。
(1)请用尺规作图作出旋转后的△ABF(不写作法,保留作图痕迹)。
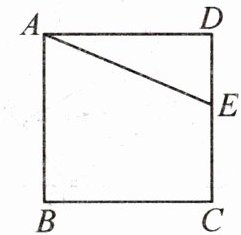
(2)连接EF,若EF=$\sqrt{34}$,DE=1,求正方形ABCD的面积。
(1)请用尺规作图作出旋转后的△ABF(不写作法,保留作图痕迹)。

(2)连接EF,若EF=$\sqrt{34}$,DE=1,求正方形ABCD的面积。
答案:
(1)
作图步骤:
以点$A$为圆心,$AD$长为半径画弧,交$AB$的延长线于点$F$(因为旋转$90^{\circ}$,$AD$旋转后与$AB$共线且$AD = AB$)。
连接$AF$,$BF$,则$\triangle ABF$即为所求(作图痕迹:弧$DF$,线段$AF$、$BF$)。
(2)
∵四边形ABCD为正方形,
∴∠BAD=90°.由旋转的性质,得AE=AF,∠EAF=∠BAD=90°.在Rt△AEF中,由勾股定理,得$AF^{2}+AE^{2}=EF^{2}$.
∴$AE^{2}=\frac{1}{2}EF^{2}=\frac{1}{2}×34=17$.在Rt△ADE中,由勾股定理,得$AD^{2}=AE^{2}-DE^{2}=17-1=16$.
∴正方形ABCD的面积为$AD^{2}=16$.
作图步骤:
以点$A$为圆心,$AD$长为半径画弧,交$AB$的延长线于点$F$(因为旋转$90^{\circ}$,$AD$旋转后与$AB$共线且$AD = AB$)。
连接$AF$,$BF$,则$\triangle ABF$即为所求(作图痕迹:弧$DF$,线段$AF$、$BF$)。
(2)
∵四边形ABCD为正方形,
∴∠BAD=90°.由旋转的性质,得AE=AF,∠EAF=∠BAD=90°.在Rt△AEF中,由勾股定理,得$AF^{2}+AE^{2}=EF^{2}$.
∴$AE^{2}=\frac{1}{2}EF^{2}=\frac{1}{2}×34=17$.在Rt△ADE中,由勾股定理,得$AD^{2}=AE^{2}-DE^{2}=17-1=16$.
∴正方形ABCD的面积为$AD^{2}=16$.
12. 现有大、小两副三角板,按照如图1所示的方式摆放,其中∠ACB=∠DEB=90°,∠B=30°,BE=AC=3。将三角板DEB绕点B按顺时针方向旋转。
(1)如图2,当点E落在边AB上时,延长DE交BC于点F,试判断BD与BF的数量关系,并说明理由。
(2)在图2中,连接AF,请求出AF的长。
]

(1)如图2,当点E落在边AB上时,延长DE交BC于点F,试判断BD与BF的数量关系,并说明理由。
(2)在图2中,连接AF,请求出AF的长。
]

答案:
12.解:
(1)BD=BF.理由:
∵∠BED=90°,
∴∠BED=∠BEF=90°.将三角板DEB绕点B按顺时针方向旋转,点E落在边AB上,
∴∠DBE=∠FBE=30°.又
∵BE=BE,
∴△BDE≌△BFE(ASA).
∴BD=BF.
(2)
∵∠ACB=90°,∠ABC=30°,AC=3,
∴AB=2AC=6.
∴BC=$\sqrt{AB^{2}-AC^{2}}$=$3\sqrt{3}$.
∵BE=3,AB=6,
∴AE=BE=3.又
∵∠BED=90°,
∴DF为AB的垂直平分线.
∴AF=BF.
∴∠ABF=∠FAB=∠CAF=30°.
∴AF=BF=2CF.
∴BC=CF+BF=3CF=$3\sqrt{3}$.
∴CF=$\sqrt{3}$.
∴AF=$2\sqrt{3}$.
(1)BD=BF.理由:
∵∠BED=90°,
∴∠BED=∠BEF=90°.将三角板DEB绕点B按顺时针方向旋转,点E落在边AB上,
∴∠DBE=∠FBE=30°.又
∵BE=BE,
∴△BDE≌△BFE(ASA).
∴BD=BF.
(2)
∵∠ACB=90°,∠ABC=30°,AC=3,
∴AB=2AC=6.
∴BC=$\sqrt{AB^{2}-AC^{2}}$=$3\sqrt{3}$.
∵BE=3,AB=6,
∴AE=BE=3.又
∵∠BED=90°,
∴DF为AB的垂直平分线.
∴AF=BF.
∴∠ABF=∠FAB=∠CAF=30°.
∴AF=BF=2CF.
∴BC=CF+BF=3CF=$3\sqrt{3}$.
∴CF=$\sqrt{3}$.
∴AF=$2\sqrt{3}$.
查看更多完整答案,请扫码查看


