《2025年名校课堂九年级数学上册人教版》

1. 新考向 传统文化 “瓦当”是中国古建筑中覆盖檐头筒瓦前端的遮挡，主要有防水、排水、保护木制飞檐和美化屋面轮廓的作用. 瓦当上的图案设计优美，字体行云流水，极富变化，是中国特有的文化艺术遗产. 下面“瓦当”图案中既是轴对称图形又是中心对称图形的是 (B)

答案： 1.B

2. 如图，已知△ABC 与△DEF 成中心对称，则对称中心是 (D)

A.点 C
B.点 E
C.线段 BC 的中点
D.线段 BE 的中点

答案： 2.D

3. 如图，这是某公园中心对称的观赏鱼池示意图，阴影部分为观赏喂鱼台，已知 OA=OB=2 米，则阴影部分的面积为$8\pi$平方米.

答案： $3.8\pi$

4. (2024·扬州)在平面直角坐标系中，点 P(1，2)关于坐标原点的对称点 P'的坐标为 (A)

A.(-1，-2)
B.(-1，2)
C.(1，-2)
D.(1，2)

答案： 4.A

5. (2024·陕西)一个正比例函数的图象经过点 A(2，m)和点 B(n，-6). 若点 A 与点 B 关于原点对称，则这个正比例函数的解析式为 (A)

A.y=3x
B.y=-3x
C.y=$\frac{1}{3}$x
D.y=-$\frac{1}{3}$x

答案： 5.A

6. 如图，在平面直角坐标系 xOy 中，△ABC 的三个顶点坐标分别为 A(-1，0)，B(-2，-2)，C(-4，-1).
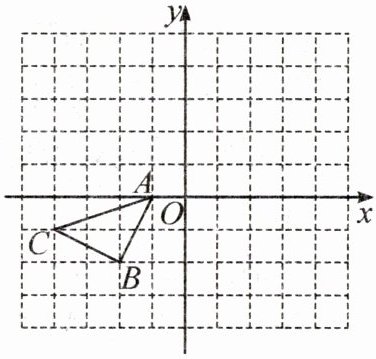
(1) 请画出△ABC 关于原点对称的△A₁B₁C₁.
(2) 将△ABC 绕点 O 逆时针旋转 90°得到△A₂B₂C₂，请画出△A₂B₂C₂.
(3) 若在△ABC 内有一点 P(a，b)，将△ABC 按照(2)中的方式旋转之后的对应点为点 P₂，则点 P₂的坐标为(- b,a).

答案： 1. （1）
关于原点对称的点的坐标特征是$(x,y)$关于原点对称的点为$(-x,-y)$。
已知$A(-1,0)$，则$A_1(1,0)$；$B(-2,-2)$，则$B_1(2,2)$；$C(-4,-1)$，则$C_1(4,1)$。
然后连接$A_1B_1$，$B_1C_1$，$C_1A_1$，得到$\triangle A_1B_1C_1$。
2. （2）
绕点$O$逆时针旋转$90^{\circ}$的坐标变化规律是$(x,y)$旋转后的坐标为$(-y,x)$。
对于$A(-1,0)$，$A_2(0, - 1)$；对于$B(-2,-2)$，$B_2(2,-2)$；对于$C(-4,-1)$，$C_2(1,-4)$。
接着连接$A_2B_2$，$B_2C_2$，$C_2A_2$，得到$\triangle A_2B_2C_2$。
3. （3）
根据绕点$O$逆时针旋转$90^{\circ}$的坐标变化规律$(x,y)\to(-y,x)$。
已知$P(a,b)$，将$\triangle ABC$绕点$O$逆时针旋转$90^{\circ}$后，点$P$的对应点$P_2$的坐标为$(-b,a)$。
综上，（1）、（2）按上述坐标画出图形；（3）答案为$(-b,a)$。

7. (2022·南充)如图，将直角三角板 ABC 绕顶点 A 顺时针旋转到△AB'C'，点 B'恰好落在 CA 的延长线上，∠B=30°，∠C=90°，则∠BAC'为 (B)

A.90°
B.60°
C.45°
D.30°

答案： 7.B

8. 如图，把四边形 ABOC 绕点 O 顺时针旋转得到四边形 DFOE，则下列角中不等于旋转角的是 (C)

A.∠BOF
B.∠AOD
C.∠COF
D.∠COE

答案： 8.C