《2025年探究学案课时卷八年级数学下册人教版》

1. 王大爷离家出门散步，他先向正北走了6m，接着又向正东走了8m，此时他离家的距离是________m.

答案： 10

2. 如图，学校有一块长方形花圃，有极少数人为了避开拐角走“捷径”，在花圃内走出了一条“路”（如图中的实线）. 其实他们仅仅少走了________m，却踩伤了花草.

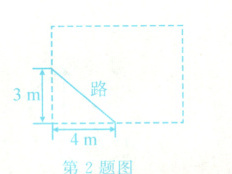
答案： 2

3. 如图，阴影部分是一个半圆，则这个半圆的面积是________（结果保留π）.
　　

答案： $\frac{9\pi}{2}$

4. 如图，一段楼梯高BC是3m，斜边AC长5m，在楼梯上铺地毯，地毯至少长________m.
　　　

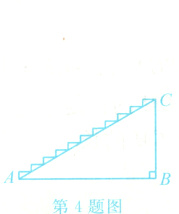
答案： 7

5. 《九章算术》是我国古代最重要的数学著作之一，在“勾股”章中记载了一道“折竹抵地”问题：“今有竹高一丈，末折抵地，去本三尺，问折者高几何？”翻译成数学问题是：如图所示，在△ABC中，∠ACB = 90°，AC + AB = 10，BC = 3，求AC的长. 如果设AC = x，则可列方程为________.
　　　

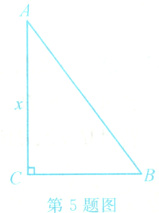
答案： $x^{2}+3^{2}=(10 - x)^{2}$

6. 在平面直角坐标系中，点P( - 4,2)到坐标原点的距离是________.

答案： $2\sqrt{5}$

7. 如图，在平面直角坐标系中，A(3,0)，B(0,2)，以点A为圆心，AB的长为半径画弧，交x轴的负半轴于点C，则点C的坐标为________.
　　　

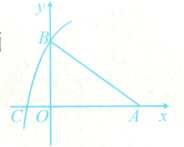
答案： $(3 - \sqrt{13},0)$

8. 在数轴上作出表示√10的点.

答案： 解:略.

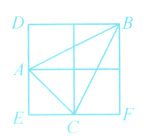
9. 如图，正方形网格中的四个小正方形的边长都为1.
（1）AC的长为________；
（2）S△ABC = ________；
（3）求点B到AC的距离h.
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

答案： 解:
(1)$\sqrt{2}$;
(2)$\frac{3}{2}$;
(3)$\frac{3\sqrt{2}}{2}$,由$S_{\triangle ABC}=\frac{1}{2}\cdot AC\cdot h$,可求$h = \frac{3\sqrt{2}}{2}$.