《2026年江苏13大市中考名卷优选38套物理》

1. (2022 镇江)如图甲所示，物体 M 静止在电梯底部，其上表面通过轻质弹簧与电梯顶部相连.M 对电梯底部的压力用 F 表示，忽略 M 和电梯的形变，0～$t_1$ 内，电梯静止，弹簧处于伸长状态，$t_1$ 时刻后电梯由静止开始沿竖直方向运动.0～$t_4$ 内，F 随时间 t 变化的图线如图乙所示，则(D)


A.$t_1$～$t_2$ 内，电梯可能向上运动
B.$t_2$～$t_3$ 内，M 的机械能保持不变
C.$t_3$～$t_4$ 内，电梯一定做加速运动
D.$t_1$～$t_4$ 内，弹簧对 M 的拉力不变

答案： 1D　物体M静止在电梯底部，弹簧处于伸长状态，0~t₁内，电梯静止，物体也处于静止，受力平衡，则受到重力G、地面的支持力F和弹簧的拉力T，由于压力与支持力是相互作用力，大小是相等的，则有G=F₂+T。当t₁~t₂内，压力变为小于F₂的F₁，弹力和重力不变，此时G＞F₁+T，则物体受力不平衡，由静止变为运动，速度变大了，则运动方向与较大的力方向相同，说明电梯是向下加速运动的，故A错误；t₂~t₃内，压力恢复到静止时的大小，说明受力平衡，因而是匀速下降，动能不变，而重力势能减小，机械能减小，故B错误；t₃~t₄内，压力F₃大于F₂，此时G＜F₃+T，电梯向下减速运动，故C错误；由于忽略M和电梯的形变，因而弹簧的长度始终不变，形变大小不变，因而弹簧的弹力保持不变，t₁~t₄内，弹簧对M的拉力不变，故D正确。

2. (2022 南通)混凝土的抗压强度与混凝土的容重有关，工程上把容重定义为 1 $m^3$ 混凝土的重.某发泡混凝土的抗压强度与其容重的关系数据如表所示.下列关于混凝土容重 $\gamma$、抗压强度 $p$ 与密度 $\rho$ 的关系图像可能正确的是 (C)

答案：
2C　根据容重定义可知，混凝土容重为$\gamma=\frac{G}{V}=\frac{mg}{V}=\rho g$，即混凝土容重$\gamma$与密度$\rho$成正比，故A、B错误；由表中数据可知，混凝土的抗压强度$p$与其容重$\gamma$的关系图大致如图所示，因为混凝土容重$\gamma$与密度$\rho$成正比，所以混凝土的抗压强度$p$与密度$\rho$的关系图像和抗压强度与容重$\gamma$的关系图像的变化趋势一样，故C正确，D错误。
　　　　　　　

3. (2024 泰州)电子技师社团活动中小明对一个暗箱进行研究.暗箱表面有两个接线柱 M、N，内部阻值未知.小明用图甲所示的电路(电源电压不变)进行实验，在 S、$S_1$ 都闭合和 S 闭合、$S_1$ 断开的两种情况下，改变电阻箱 $R_0$ 的阻值，读取电流表示数 I，绘制了如图乙所示的 I 随 $R_0$ 变化的曲线.下列判断中正确的是 (D)


A.电源电压为 8 V
B.电阻 $R_2$ 的阻值是 20 $\Omega$
C.曲线 A 是根据开关 S、$S_1$ 都闭合时测得的实验数据绘制的
D.暗箱内电阻 $R_1$ 与 $R_2$ 是串联连接的

答案： 3D　由图甲可知，在开关S、S₁都闭合时，电路为电阻箱R₀的简单电路，此时电阻箱接入电路的电阻不能为零，否则会造成电源短路，所以可判断曲线B为S、S₁都闭合时的图像，则曲线A为开关S闭合、S₁断开的图像。电源电压$U = IR_0 = 1.4A×30Ω = 42V$，故A、C错误；曲线A为开关S闭合、S₁断开的图像，此时电阻箱和暗箱串联，当电流表示数$I = 1.4A$时，该电路的总电阻$R_{总}=\frac{U}{I}=\frac{42V}{1.4A}=30Ω$，暗箱内的电阻$R' = R_{总}-R_{0}=30Ω - 20Ω = 10Ω＞6Ω$，所以暗箱内电阻R₁与R₂是串联的，且R₂的阻值为$R_{2}=R'-R_{1}=10Ω - 6Ω = 4Ω$，故B错误，D正确。

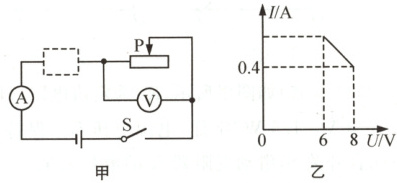
4. (2024 苏州)图甲中，电源电压为 12 V、电流表(0～0.6 A)、电压表(0～15 V)、滑动变阻器标有“？$\Omega$ 1 A”字样，虚线框内是一个定值电阻或是一个小灯泡(6 V 0.5 A)闭合开关，在元件安全的情况下，使滑片 P 移动范围最大，得到滑动变阻器的 I-U 图像如图乙所示.则：
①虚线框内是小灯泡；
②电路的最大功率为 6 W；
③虚线框内元件和滑动变阻器的功率相等时，滑动变阻器的阻值为 10 $\Omega$；
④滑动变阻器最大阻值为 20 $\Omega$.
以上结论正确的是
(A)


A.③④
B.②③
C.①②
D.①④

答案： 4A　由电路图可知，定值电阻或小灯泡与滑动变阻器串联，电流表测量电路中的电流，电压表测量滑动变阻器两端的电压。根据欧姆定律可得，滑动变阻器的I - U关系式为$I = I_{定}=\frac{U_{定}}{R_{定}}=\frac{U_{电}-U}{R_{定}}=\frac{U_{电}}{R_{定}}-\frac{U}{R_{定}}$或$I = I_{L}=\frac{U_{L}}{R_{L}}=\frac{U_{电}-U}{R_{L}}=\frac{U_{电}}{R_{L}}-\frac{U}{R_{L}}$，由图乙可知，滑动变阻器的I - U关系为一次函数关系，则虚线框内的元件阻值为一定值，由于小灯泡的电阻随温度的变化而变化，不是一个定值，所以虚线框内是定值电阻，不是小灯泡，故①错误；由于电压表最大量程大于电源电压，故滑动变阻器的滑片可以移动到最大阻值处，由图乙可知，滑动变阻器两端的电压最大为$U_{max}=8V$，通过电路的最小电流为$I_{min}=0.4A$，则滑动变阻器的最大阻值为$R_{max}=\frac{U_{max}}{I_{min}}=\frac{8V}{0.4A}=20Ω$，故④正确；此时定值电阻两端的电压为$U_{定}=U_{电}-U_{max}=12V - 8V = 4V$，定值电阻的阻值为$R_{定}=\frac{U_{定}}{I_{min}}=\frac{4V}{0.4A}=10Ω$，当滑动变阻器两端的电压最小时，电路中的电流最大，此时定值电阻两端的电压为$U_{定}'=U_{电}-U_{min}=12V - 6V = 6V$，电路中的最大电流为$I_{max}=I_{定}'=\frac{U_{定}'}{R_{定}}=\frac{6V}{10Ω}=0.6A$，电路的最大功率为$P_{max}=U_{电}I_{max}=12V×0.6A = 7.2W$，故②错误；串联电路各处电流相等，当$P_{定}=P_{滑}$时，由$P = UI = I^{2}R$可知，定值电阻与滑动变阻器两端的电压相等，根据串联电路的分压原理可知，滑动变阻器接入电路的阻值与定值电阻的阻值相等，为$10Ω$，故③正确；故选A。

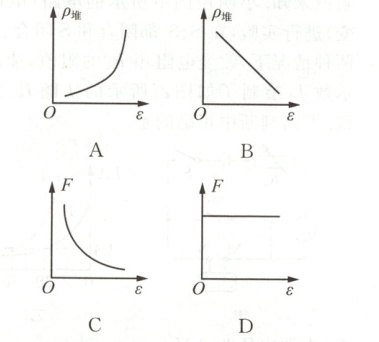
5. (2023 南通)如图所示，固体颗粒放入容器中，颗粒间有孔隙.材料学上把孔隙体积与颗粒和孔隙总体积的比值称为孔隙率 $\epsilon$，把颗粒质量与颗粒和孔隙总体积的比值称为堆密度 $\rho_{堆}$.将同种物质制成的大小不同的颗粒分别装满同一容器后，下列描述堆密度 $\rho_{堆}$、容器对水平桌面的压力 $F$ 与孔隙率 $\epsilon$ 的关系图线中，可能正确的是 (B)

答案： 5B　孔隙体积与颗粒和孔隙总体积的比值称为孔隙率$\epsilon$，假设容器的体积为V，装满后，颗粒的体积为$(1 - \epsilon)V$，整体的质量等于颗粒的质量，$m = \rho_{实}(1 - \epsilon)V$，堆密度$\rho_{堆}=\frac{m}{V}=\frac{\rho_{实}(1 - \epsilon)V}{V}=\rho_{实}(1 - \epsilon)$，由于颗粒实心的密度不变，则堆密度$\rho_{堆}$与孔隙率$\epsilon$成一次函数关系，且随着$\epsilon$的增大而减小，A错误，B正确；容器对水平桌面的压力F等于容器重力和颗粒物的总重力，$F = G_{容}+mg = G_{容}+\rho_{实}(1 - \epsilon)Vg$，也是一次函数关系，且随着$\epsilon$的增大而减小，C、D错误。