2026年金考卷中考45套汇编数学河北专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年金考卷中考45套汇编数学河北专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第90页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
23. (本小题满分11分)
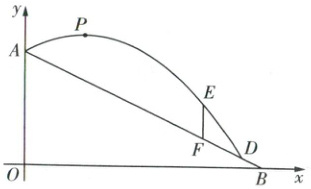
冬奥会带动了滑雪运动的兴起,嘉嘉所在城市新建滑雪场,嘉嘉依据滑雪场地,以地面($OB$所在直线)为$x$轴,过起跳点$A$作$x$轴的垂线为$y$轴,构建如图所示的平面直角坐标系,$OA = 60$米.有一运动员通过助滑坡后从起跳点$A$处腾空跃起,沿运动轨迹$APD$运动,最后着陆在滑道$AB$上的点$D$处,然后继续向$B$点滑行,$OB = 120$米.将运动员看作一点,其空中运动轨迹$APD$段可近似看作抛物线$y = -\frac{1}{100}x^{2}+bx + c$的一部分,已知点$P$为运动员在空中的最高点,点$D$为着陆点,且其到地面($OB$所在直线)的距离为$5$米.
(1)求点$D$坐标.
(2)求抛物线的解析式,并直接写出点$P$坐标.
(3)现该运动员从最高点$P$处开始做转体动作,已知要完整做完这个转体动作,从开始转体到动作结束至少需$40$米的垂直距离.为保证在点$D$处安全着陆,该运动员必须在位于点$F$($F$为滑道$AB$上一点)正上方$18$米高度的点$E$处停止做转体动作,准备着陆.请通过计算说明该运动员能否完整做完这个转体动作.
冬奥会带动了滑雪运动的兴起,嘉嘉所在城市新建滑雪场,嘉嘉依据滑雪场地,以地面($OB$所在直线)为$x$轴,过起跳点$A$作$x$轴的垂线为$y$轴,构建如图所示的平面直角坐标系,$OA = 60$米.有一运动员通过助滑坡后从起跳点$A$处腾空跃起,沿运动轨迹$APD$运动,最后着陆在滑道$AB$上的点$D$处,然后继续向$B$点滑行,$OB = 120$米.将运动员看作一点,其空中运动轨迹$APD$段可近似看作抛物线$y = -\frac{1}{100}x^{2}+bx + c$的一部分,已知点$P$为运动员在空中的最高点,点$D$为着陆点,且其到地面($OB$所在直线)的距离为$5$米.
(1)求点$D$坐标.
(2)求抛物线的解析式,并直接写出点$P$坐标.
(3)现该运动员从最高点$P$处开始做转体动作,已知要完整做完这个转体动作,从开始转体到动作结束至少需$40$米的垂直距离.为保证在点$D$处安全着陆,该运动员必须在位于点$F$($F$为滑道$AB$上一点)正上方$18$米高度的点$E$处停止做转体动作,准备着陆.请通过计算说明该运动员能否完整做完这个转体动作.

答案:
(1)由题意可知A(0,60),B(120,0)。
设AB所在直线的解析式为y = kx + m,
则{120k + m = 0,m = 60},解得{k = -1/2,m = 60}
∴AB所在直线的解析式为y = -1/2x + 60。
令y = 5,即 -1/2x + 60 = 5(点拨:此方程的解为点D的横坐标),解得x = 110,
∴D(110,5)。(4分)
(2)将A(0,60),D(110,5)分别代入y = -1/100x² + bx + c,
得{-1/100×110² + 110b + c = 5,c = 60},解得{b = 0.6,c = 60}
∴抛物线的解析式为y = -0.01x² + 0.6x + 60 = -0.01(x-30)²+69,
∴P(30,69)。(8分)
(3)令 -0.01x² + 0.6x + 60 - (-1/2x + 60) = 18(点拨:列方程求点F的横坐标),
整理,得x² - 110x + 1800 = 0,解得x₁ = 20,x₂ = 90。
∵点F在抛物线的对称轴右侧,
∴点F的横坐标是90。
当x = 90时,y = -0.01x² + 0.6x + 60 = 33。
∵69 - 33 = 36<40,
∴该运动员不能完整做完这个转体动作。(11分)
(1)由题意可知A(0,60),B(120,0)。
设AB所在直线的解析式为y = kx + m,
则{120k + m = 0,m = 60},解得{k = -1/2,m = 60}
∴AB所在直线的解析式为y = -1/2x + 60。
令y = 5,即 -1/2x + 60 = 5(点拨:此方程的解为点D的横坐标),解得x = 110,
∴D(110,5)。(4分)
(2)将A(0,60),D(110,5)分别代入y = -1/100x² + bx + c,
得{-1/100×110² + 110b + c = 5,c = 60},解得{b = 0.6,c = 60}
∴抛物线的解析式为y = -0.01x² + 0.6x + 60 = -0.01(x-30)²+69,
∴P(30,69)。(8分)
(3)令 -0.01x² + 0.6x + 60 - (-1/2x + 60) = 18(点拨:列方程求点F的横坐标),
整理,得x² - 110x + 1800 = 0,解得x₁ = 20,x₂ = 90。
∵点F在抛物线的对称轴右侧,
∴点F的横坐标是90。
当x = 90时,y = -0.01x² + 0.6x + 60 = 33。
∵69 - 33 = 36<40,
∴该运动员不能完整做完这个转体动作。(11分)
24. (本小题满分12分)
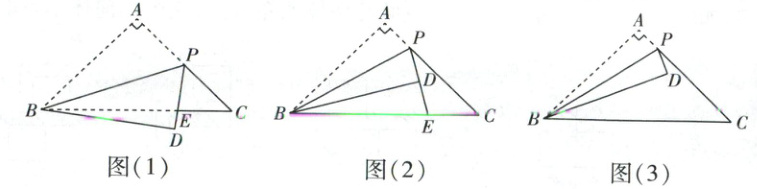
如图,$\mathrm{Rt}\triangle ABC$中,$\angle A = 90^{\circ}$,$AB = AC = 4$,$P$为$AC$边上一点(不含端点),将$\triangle ABC$沿$BP$折叠,点$A$落在点$D$处,连接$BD$,$PD$,直线$PD$与$BC$边交于点$E$,设$AP = x$.
(1)当$\angle DBC = 5^{\circ}$时,$\angle DPC=$
(2)如图(1),当$P$为$AC$的中点时,求$\tan\angle PBC$的值;
(3)如图(2),当$BD$平分$\angle PBC$时,请直接写出$\angle DPC$的度数并求出此时$x$的值;
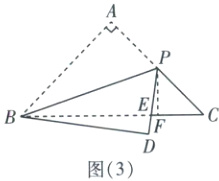
(4)如图(3),当点$D$在$BC$上时,请直接写出点$D$到$BC$的距离(用含$x$的代数式表示).
如图,$\mathrm{Rt}\triangle ABC$中,$\angle A = 90^{\circ}$,$AB = AC = 4$,$P$为$AC$边上一点(不含端点),将$\triangle ABC$沿$BP$折叠,点$A$落在点$D$处,连接$BD$,$PD$,直线$PD$与$BC$边交于点$E$,设$AP = x$.
(1)当$\angle DBC = 5^{\circ}$时,$\angle DPC=$
40°或50°
;(2)如图(1),当$P$为$AC$的中点时,求$\tan\angle PBC$的值;
(3)如图(2),当$BD$平分$\angle PBC$时,请直接写出$\angle DPC$的度数并求出此时$x$的值;
(4)如图(3),当点$D$在$BC$上时,请直接写出点$D$到$BC$的距离(用含$x$的代数式表示).

答案:
(1)40°或50° (4分)
解法提示:由折叠知∠BDP = ∠A = 90°。
分两种情况讨论。
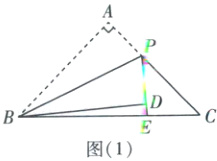
①当点D在BC上方时,如图
(1)。
∵∠BDE = 180° - ∠BDP = 90°,
∴∠PEC = ∠BDE + ∠DBC = 90° + 5° = 95°,
∴∠DPC = 180° - ∠PEC - ∠C = 180° - 95° - 45° = 40°。
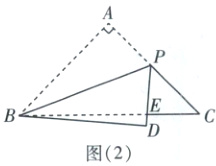
②如图
(2),当点D在BC下方时。
∵∠BED = ∠PEC,三角形的内角和是180°,
∴∠DBE + ∠D = ∠DPC + ∠C,即5° + 90° = ∠DPC + 45°,
∴∠DPC = 50°。
综上所述,∠DPC = 40°或50°。
(2)如图
(3),过点P作PF⊥BC于点F。
∵P是AC的中点,
∴PC = 1/2AC = 2。
∵∠A = 90°,AB = AC,
∴∠C = 45°,
∴FC = PF = PC·sin45° = 2×√2/2 = √2,BC = AB/sin45° = 4/(√2/2) = 4√2,
∴BF = BC - FC = 4√2 - √2 = 3√2,
∴tan∠PBC = PF/BF = √2/(3√2) = 1/3。(7分)
(3)∠DPC = 30°。(8分)
由折叠的性质,得DP = AP = x,∠BDP = ∠A = 90°。
∵∠PBD = ∠EBD,∠PDB = ∠EDB = 90°,BD = BD,
∴△PDB≌△EDB,
∴DE = DP = x,
∴PE = 2x。
如图
(4),过点E作EG⊥AC于点G,
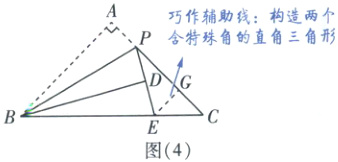
∵∠DPC = 30°,∠C = 45°,
∴EG = 1/2PE = x,PG = √3/2PE = √3x,GC = EG = x。
∵AC = AP + PG + GC = 4,
∴x + √3x + x = 4,
∴x = 4/(2+√3) = 4×(2-√3) = 8 - 4√3。(11分)
一题多解
本问还可以用如下方法求x的值:
如图,过点P作PM⊥BC于点M。
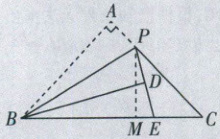
在Rt△PMC中,∠C = 45°,CP = 4 - x,
∴PM = √2/2CP = √2/2(4 - x)。
∵∠DBE = ∠DBP = ∠ABP,∠ABC = 45°,
∴∠DBE = ∠DBP = ∠ABP = 15°,
∴∠MBP = 30°,
∴BP = 2PM = √2(4 - x)。
在Rt△ABP中,AB = 4,AP = x,
∴BP² = x² + 16,
∴x² + 16 = 2(4 - x)²,
解得x₁ = 8 - 4√3,x₂ = 8 + 4√3(不合题意,舍去),
∴x = 8 - 4√3。
(4)点D到BC的距离为(-2√2x² - 16√2x + 32√2)/(x²+16) (12分)
快招解题法 试题秒解 考场速用
本问可利用“等面积法”列方程求解,解法提示如下:
如图
(5),连接AD交BP于点H,连接CD,过点D分别作DJ⊥BC于点J,DK⊥PC于点K(点拨:点D实质为△ABC内一动点,DJ不易直接求解,故考虑在△ABC中用“等面积法”求解,故分割△ABC),则BP垂直平分AD。
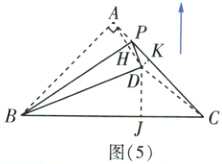
将△ABC的面积分割成△ABP、△CPD、△BDC的面积之和,故求出DK的长后即可求出DJ的长。
在Rt△ABP中,AB = 4,AP = x,
∴BP = √(x²+16)
∵S△ABP = 1/2AB·AP = 1/2BP·AH(点拨:在△ABP中,利用“等面积法”得到关于AH的方程(本题中x看作已知数))
∴AH = AB·AP/BP = 4x/√(x²+16),
∴AD = 2AH = 8x/√(x²+16)
易证∠DAK = ∠ABP,
∴sin∠DAK = sin∠ABP,
∴DK/AD = AP/BP,
∴DK = 8x²/(x²+16)
∵S△ABC = 2S△ABP + S△CPD + S△BDC,即1/2AB·AC = 2×1/2AB·AP + 1/2PC·DK + 1/2BC·DJ,
∴1/2×4×4 = 4x + 1/2×(4 - x)×8x²/(x²+16) + 1/2×4√2×DJ(点拨:在△ABC中,利用“等面积法”得到关于DJ的方程)
∴DJ = (-2√2x² - 16√2x + 32√2)/(x²+16)
即点D到BC的距离为(-2√2x² - 16√2x + 32√2)/(x²+16)
更多讲解详见《解题有招》折页“快招3”
(1)40°或50° (4分)
解法提示:由折叠知∠BDP = ∠A = 90°。
分两种情况讨论。
①当点D在BC上方时,如图
(1)。
∵∠BDE = 180° - ∠BDP = 90°,
∴∠PEC = ∠BDE + ∠DBC = 90° + 5° = 95°,
∴∠DPC = 180° - ∠PEC - ∠C = 180° - 95° - 45° = 40°。

②如图
(2),当点D在BC下方时。
∵∠BED = ∠PEC,三角形的内角和是180°,
∴∠DBE + ∠D = ∠DPC + ∠C,即5° + 90° = ∠DPC + 45°,
∴∠DPC = 50°。

综上所述,∠DPC = 40°或50°。
(2)如图
(3),过点P作PF⊥BC于点F。

∵P是AC的中点,
∴PC = 1/2AC = 2。
∵∠A = 90°,AB = AC,
∴∠C = 45°,
∴FC = PF = PC·sin45° = 2×√2/2 = √2,BC = AB/sin45° = 4/(√2/2) = 4√2,
∴BF = BC - FC = 4√2 - √2 = 3√2,
∴tan∠PBC = PF/BF = √2/(3√2) = 1/3。(7分)
(3)∠DPC = 30°。(8分)
由折叠的性质,得DP = AP = x,∠BDP = ∠A = 90°。
∵∠PBD = ∠EBD,∠PDB = ∠EDB = 90°,BD = BD,
∴△PDB≌△EDB,
∴DE = DP = x,
∴PE = 2x。
如图
(4),过点E作EG⊥AC于点G,

∵∠DPC = 30°,∠C = 45°,
∴EG = 1/2PE = x,PG = √3/2PE = √3x,GC = EG = x。
∵AC = AP + PG + GC = 4,
∴x + √3x + x = 4,
∴x = 4/(2+√3) = 4×(2-√3) = 8 - 4√3。(11分)
一题多解
本问还可以用如下方法求x的值:
如图,过点P作PM⊥BC于点M。

在Rt△PMC中,∠C = 45°,CP = 4 - x,
∴PM = √2/2CP = √2/2(4 - x)。
∵∠DBE = ∠DBP = ∠ABP,∠ABC = 45°,
∴∠DBE = ∠DBP = ∠ABP = 15°,
∴∠MBP = 30°,
∴BP = 2PM = √2(4 - x)。
在Rt△ABP中,AB = 4,AP = x,
∴BP² = x² + 16,
∴x² + 16 = 2(4 - x)²,
解得x₁ = 8 - 4√3,x₂ = 8 + 4√3(不合题意,舍去),
∴x = 8 - 4√3。
(4)点D到BC的距离为(-2√2x² - 16√2x + 32√2)/(x²+16) (12分)
快招解题法 试题秒解 考场速用
本问可利用“等面积法”列方程求解,解法提示如下:
如图
(5),连接AD交BP于点H,连接CD,过点D分别作DJ⊥BC于点J,DK⊥PC于点K(点拨:点D实质为△ABC内一动点,DJ不易直接求解,故考虑在△ABC中用“等面积法”求解,故分割△ABC),则BP垂直平分AD。

将△ABC的面积分割成△ABP、△CPD、△BDC的面积之和,故求出DK的长后即可求出DJ的长。
在Rt△ABP中,AB = 4,AP = x,
∴BP = √(x²+16)
∵S△ABP = 1/2AB·AP = 1/2BP·AH(点拨:在△ABP中,利用“等面积法”得到关于AH的方程(本题中x看作已知数))
∴AH = AB·AP/BP = 4x/√(x²+16),
∴AD = 2AH = 8x/√(x²+16)
易证∠DAK = ∠ABP,
∴sin∠DAK = sin∠ABP,
∴DK/AD = AP/BP,
∴DK = 8x²/(x²+16)
∵S△ABC = 2S△ABP + S△CPD + S△BDC,即1/2AB·AC = 2×1/2AB·AP + 1/2PC·DK + 1/2BC·DJ,
∴1/2×4×4 = 4x + 1/2×(4 - x)×8x²/(x²+16) + 1/2×4√2×DJ(点拨:在△ABC中,利用“等面积法”得到关于DJ的方程)
∴DJ = (-2√2x² - 16√2x + 32√2)/(x²+16)
即点D到BC的距离为(-2√2x² - 16√2x + 32√2)/(x²+16)
更多讲解详见《解题有招》折页“快招3”
查看更多完整答案,请扫码查看


