2026年金考卷中考45套汇编数学河北专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年金考卷中考45套汇编数学河北专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第35页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
21. (本小题满分9分)
某物流公司推行环保运输政策,通过分段计价引导客户集约化运输,并制定如下计价规则。
|计价规则|
|--|
|货物质量不超过10kg时,单价为6元/kg;|
|货物质量超过10kg但不超过20kg时,超过10kg部分单价为5元/kg;|
|货物质量超出20kg时,超出20kg的部分单价为4元/kg,并一次性额外收取30元的碳排放附加费。|
设货物质量为$x$(kg),运费为$y$(元)。
(1)若货物A质量为8kg,货物B质量为15kg,分别计算两个货物的运费;
(2)当$x > 20$时,求$y$与$x$之间的函数关系式;
(3)若某货物的运费为170元,求该货物质量为多少。
某物流公司推行环保运输政策,通过分段计价引导客户集约化运输,并制定如下计价规则。
|计价规则|
|--|
|货物质量不超过10kg时,单价为6元/kg;|
|货物质量超过10kg但不超过20kg时,超过10kg部分单价为5元/kg;|
|货物质量超出20kg时,超出20kg的部分单价为4元/kg,并一次性额外收取30元的碳排放附加费。|
设货物质量为$x$(kg),运费为$y$(元)。
(1)若货物A质量为8kg,货物B质量为15kg,分别计算两个货物的运费;
(2)当$x > 20$时,求$y$与$x$之间的函数关系式;
(3)若某货物的运费为170元,求该货物质量为多少。
答案:
21. 名师教审题
函数的实际应用题系列。本题为分段计费问题,各段收费规则如下:
货物质量 收费标准
第一段 不超过10kg的部分 6元/kg
第二段 超过10kg但不超过20kg的部分 5元/kg
第三段 超过20kg的部分 4元/kg,并额外收取30元
(1)当x = 8时,y = 8×6 = 48;
当x = 15时,y = 6×10 + 5×(15 - 10) = 85。
答:货物A的运费为48元,货物B的运费为85元。
(2)由题意可得,当x>20时,y = 6×10 + 5×10 + 4(x - 20) + 30 = 4x + 60。
(3)
∵当x = 20时,y = 6×10 + 5×10 = 110<170,
∴当运费为170元时,x>20,
∴4x + 60 = 170,解得x = 27.5。
答:该货物质量为27.5千克。
函数的实际应用题系列。本题为分段计费问题,各段收费规则如下:
货物质量 收费标准
第一段 不超过10kg的部分 6元/kg
第二段 超过10kg但不超过20kg的部分 5元/kg
第三段 超过20kg的部分 4元/kg,并额外收取30元
(1)当x = 8时,y = 8×6 = 48;
当x = 15时,y = 6×10 + 5×(15 - 10) = 85。
答:货物A的运费为48元,货物B的运费为85元。
(2)由题意可得,当x>20时,y = 6×10 + 5×10 + 4(x - 20) + 30 = 4x + 60。
(3)
∵当x = 20时,y = 6×10 + 5×10 = 110<170,
∴当运费为170元时,x>20,
∴4x + 60 = 170,解得x = 27.5。
答:该货物质量为27.5千克。
22. (本小题满分9分)
背景:如图(1)是文具店正在销售的某种文件夹,图(2)为该文件夹装入纸张前后的纵截面示意图,已知纸张与
测量:如图(2)(甲),未装入纸张时,点$B$落在$MN$上,此时$\angle BPH = 30^{\circ}$。如图(2)(乙),装满纸张时,点$A$落在$MN$上,此时$\angle APH = 45^{\circ}$。
计算:借助以上信息,解决下列问题:(计算结果保留根号)
(1)求夹纸板截线$PB$与扣板截线$PA$的长;
(2)如图(2)(丙),装入30张纸后测得$\angle APH = 75^{\circ}$,若每张纸厚度相等,求每张纸的厚度;
(3)直接写出未装入纸张时$A$,$H$两点之间的距离。
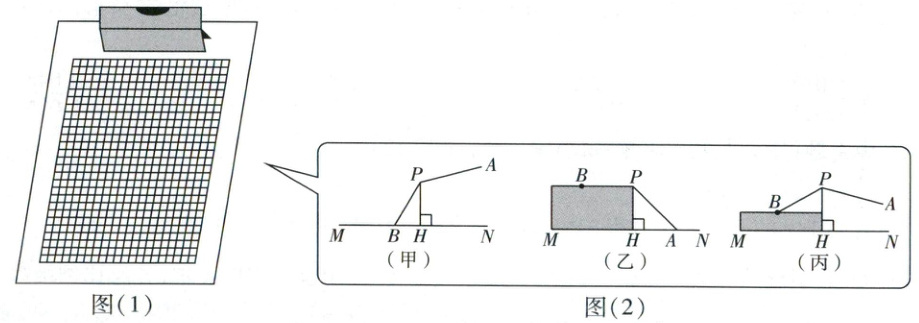
背景:如图(1)是文具店正在销售的某种文件夹,图(2)为该文件夹装入纸张前后的纵截面示意图,已知纸张与
龙
骨截线$PH$垂直,且$PH$垂直于底板$MN$,$PH = 6$mm,夹纸板截线$PB$与扣板截线$PA$的夹角始终保持$135^{\circ}$。测量:如图(2)(甲),未装入纸张时,点$B$落在$MN$上,此时$\angle BPH = 30^{\circ}$。如图(2)(乙),装满纸张时,点$A$落在$MN$上,此时$\angle APH = 45^{\circ}$。
计算:借助以上信息,解决下列问题:(计算结果保留根号)
(1)求夹纸板截线$PB$与扣板截线$PA$的长;
(2)如图(2)(丙),装入30张纸后测得$\angle APH = 75^{\circ}$,若每张纸厚度相等,求每张纸的厚度;
(3)直接写出未装入纸张时$A$,$H$两点之间的距离。

答案:
22. 名师教审题解直角三角形的实际应用题系列审题后,将获取的信息在图中标注出来,如下:


(1)在题图
(2)(甲)中,
∵∠BPH = 30°,PH = 6mm,
∴PB = $\frac{PH}{cos30°}$ = 6÷$\frac{\sqrt{3}}{2}$ = 4$\sqrt{3}$(mm)。
在题图
(2)(乙)中,
∵∠APH = 45°,PH = 6mm,
∴PA = $\frac{PH}{cos45°}$ = 6÷$\frac{\sqrt{2}}{2}$ = 6$\sqrt{2}$(mm)。
(2)如图
(1),设纸张的上边缘与PH交于点Q,由题意知BQ⊥PH。

∵∠BPA = 135°,∠APH = 75°,
∴∠BPH = 60°。
又
∵PB = 4$\sqrt{3}$mm,
∴PQ = PB·cos60° = 4$\sqrt{3}$×$\frac{1}{2}$ = 2$\sqrt{3}$(mm),
∴HQ = (6 - 2$\sqrt{3}$)mm,
∴每张纸的厚度为$\frac{6 - 2\sqrt{3}}{30}$ = $\frac{3 - \sqrt{3}}{15}$(mm)。
(3)(3$\sqrt{2}$ + 3$\sqrt{6}$)mm。
解法提示:
如图
(2),连接AH,过点A作AC⊥HP于点C,在HN上取点K,使PH = HK,连接PK,AK,则∠1 = 45°,PK = 6$\sqrt{2}$ = AP,
巧作辅助线:①欲求AH,则构造Rt△ACH;
②猜想AC = CH,故构造等边三角形APK。

∴∠2 = 135° - 30° - 45° = 60°,
∴△APK是等边三角形(依据:一个内角是60°的等腰三角形是等边三角形),
∴AP = AK;
又
∵PH = HK,
∴AH垂直平分线段PK(依据:到线段两端距离相等的点在线段的垂直平分线上),
∴∠AHC = 45°,
∴AC = CH;
设PC = x,则AC = CH = x + 6。
∵PC² + AC² = AP²,
∴x² + (x + 6)² = (6$\sqrt{2}$)²,解得x = 3$\sqrt{3}$ - 3(负值已舍),
∴CH = x + 6 = 3$\sqrt{3}$ + 3,
∴AH = $\sqrt{2}$CH = (3$\sqrt{2}$ + 3$\sqrt{6}$)mm。
第
(3)问还可按如下方法:
如图,连接AH,过点A作AC⊥HP于点C
巧作辅助线:①欲求AH,则构造Rt△ACH
②∠APC = 75°,故构造等腰三角形APD从

∵∠BPA = 135°,∠BPH = 30°,
∴∠HPA = ∠BPA - ∠BPH = 135° - 30° = 105°,
∴∠CPA = 75°,∠CAP = 15°。
在AC上取一点D使AD = PD,连接PD
则∠DPA = ∠CAP = 15°(依据:等边对等角)
∴∠CDP = ∠CAP + ∠DPA = 30°(依据:三角形的外角等于与它不相邻的两内角的和)
设PC = x,则AD = PD = 2PC = 2x,CD = $\sqrt{3}$PC = $\sqrt{3}$x
∴AC = AD + CD = 2x + $\sqrt{3}$x = (2 + $\sqrt{3}$)x。
在Rt△ACP中,AC² + CP² = AP²,即(2 + $\sqrt{3}$)²x² + x² = (6$\sqrt{2}$)²,
x² = 36 - 18$\sqrt{3}$ = 9(4 - 2$\sqrt{3}$) = 9($\sqrt{3}$ - 1)²,
x = 3($\sqrt{3}$ - 1) = 3$\sqrt{3}$ - 3
∴AC = (2 + $\sqrt{3}$)x = 3 + 3$\sqrt{3}$,CH = 3$\sqrt{3}$ - 3 + 6 = 3 + 3$\sqrt{3}$
∴△ACH是等腰直角三角形
∴AH = $\sqrt{2}$AC = (3$\sqrt{2}$ + 3$\sqrt{6}$)mm。
22. 名师教审题解直角三角形的实际应用题系列审题后,将获取的信息在图中标注出来,如下:


(1)在题图
(2)(甲)中,
∵∠BPH = 30°,PH = 6mm,
∴PB = $\frac{PH}{cos30°}$ = 6÷$\frac{\sqrt{3}}{2}$ = 4$\sqrt{3}$(mm)。
在题图
(2)(乙)中,
∵∠APH = 45°,PH = 6mm,
∴PA = $\frac{PH}{cos45°}$ = 6÷$\frac{\sqrt{2}}{2}$ = 6$\sqrt{2}$(mm)。
(2)如图
(1),设纸张的上边缘与PH交于点Q,由题意知BQ⊥PH。

∵∠BPA = 135°,∠APH = 75°,
∴∠BPH = 60°。
又
∵PB = 4$\sqrt{3}$mm,
∴PQ = PB·cos60° = 4$\sqrt{3}$×$\frac{1}{2}$ = 2$\sqrt{3}$(mm),
∴HQ = (6 - 2$\sqrt{3}$)mm,
∴每张纸的厚度为$\frac{6 - 2\sqrt{3}}{30}$ = $\frac{3 - \sqrt{3}}{15}$(mm)。
(3)(3$\sqrt{2}$ + 3$\sqrt{6}$)mm。
解法提示:
如图
(2),连接AH,过点A作AC⊥HP于点C,在HN上取点K,使PH = HK,连接PK,AK,则∠1 = 45°,PK = 6$\sqrt{2}$ = AP,
巧作辅助线:①欲求AH,则构造Rt△ACH;
②猜想AC = CH,故构造等边三角形APK。

∴∠2 = 135° - 30° - 45° = 60°,
∴△APK是等边三角形(依据:一个内角是60°的等腰三角形是等边三角形),
∴AP = AK;
又
∵PH = HK,
∴AH垂直平分线段PK(依据:到线段两端距离相等的点在线段的垂直平分线上),
∴∠AHC = 45°,
∴AC = CH;
设PC = x,则AC = CH = x + 6。
∵PC² + AC² = AP²,
∴x² + (x + 6)² = (6$\sqrt{2}$)²,解得x = 3$\sqrt{3}$ - 3(负值已舍),
∴CH = x + 6 = 3$\sqrt{3}$ + 3,
∴AH = $\sqrt{2}$CH = (3$\sqrt{2}$ + 3$\sqrt{6}$)mm。
第
(3)问还可按如下方法:
如图,连接AH,过点A作AC⊥HP于点C
巧作辅助线:①欲求AH,则构造Rt△ACH
②∠APC = 75°,故构造等腰三角形APD从

∵∠BPA = 135°,∠BPH = 30°,
∴∠HPA = ∠BPA - ∠BPH = 135° - 30° = 105°,
∴∠CPA = 75°,∠CAP = 15°。
在AC上取一点D使AD = PD,连接PD
则∠DPA = ∠CAP = 15°(依据:等边对等角)
∴∠CDP = ∠CAP + ∠DPA = 30°(依据:三角形的外角等于与它不相邻的两内角的和)
设PC = x,则AD = PD = 2PC = 2x,CD = $\sqrt{3}$PC = $\sqrt{3}$x
∴AC = AD + CD = 2x + $\sqrt{3}$x = (2 + $\sqrt{3}$)x。
在Rt△ACP中,AC² + CP² = AP²,即(2 + $\sqrt{3}$)²x² + x² = (6$\sqrt{2}$)²,
x² = 36 - 18$\sqrt{3}$ = 9(4 - 2$\sqrt{3}$) = 9($\sqrt{3}$ - 1)²,
x = 3($\sqrt{3}$ - 1) = 3$\sqrt{3}$ - 3
∴AC = (2 + $\sqrt{3}$)x = 3 + 3$\sqrt{3}$,CH = 3$\sqrt{3}$ - 3 + 6 = 3 + 3$\sqrt{3}$
∴△ACH是等腰直角三角形
∴AH = $\sqrt{2}$AC = (3$\sqrt{2}$ + 3$\sqrt{6}$)mm。
查看更多完整答案,请扫码查看


