2026年金考卷中考45套汇编数学河北专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年金考卷中考45套汇编数学河北专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
15. 新题型 代数推理题“铺地锦”是我国古代一种乘法运算方法,可将多位数乘法运算转化为一位数乘法和简单的加法运算.淇淇受其启发,设计了如图(1)所示的“表格算法”,图(1)表示$132×23$,运算结果为3036.图(2)表示一个三位数与一个两位数相乘,表格中部分数据被墨迹覆盖,根据图(2)中现有数据进行推断,正确的是(
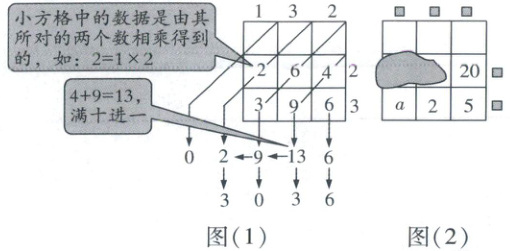
A.“20”左边的数是16
B.“20”右边的“□”表示5
C.运算结果小于6000
D.运算结果可以表示为$4100a + 1025$
D
)
A.“20”左边的数是16
B.“20”右边的“□”表示5
C.运算结果小于6000
D.运算结果可以表示为$4100a + 1025$
答案:
15 D 设题图
(2)表示三位数$(100x + 10y + z)$和两位数$(10m + n)$相乘,如图
(1)所示.根据题图
(1)所示的“表格算法”,可知$ny = 2$,$nz = 5$(点拨:$2 = 1× 2$,$5 = 1× 5$,故尝试以此为突破口解题).又$\because n,y,z$是正整数,$\therefore n = 1$,$y = 2$,$z = 5$,$\therefore x = a.\because zm = 20$,$\therefore m = 4$,故B错误.如图
(2),易知“20”左边的数是$2× 4 = 8$,故A错误.运算结果为$(100x + 10y + z)(10m + n)=(100a + 25)× 41 = 4100a + 1025$,故D正确.易知当$a\geqslant 2$时,运算结果大于6000,故C错误.


15 D 设题图
(2)表示三位数$(100x + 10y + z)$和两位数$(10m + n)$相乘,如图
(1)所示.根据题图
(1)所示的“表格算法”,可知$ny = 2$,$nz = 5$(点拨:$2 = 1× 2$,$5 = 1× 5$,故尝试以此为突破口解题).又$\because n,y,z$是正整数,$\therefore n = 1$,$y = 2$,$z = 5$,$\therefore x = a.\because zm = 20$,$\therefore m = 4$,故B错误.如图
(2),易知“20”左边的数是$2× 4 = 8$,故A错误.运算结果为$(100x + 10y + z)(10m + n)=(100a + 25)× 41 = 4100a + 1025$,故D正确.易知当$a\geqslant 2$时,运算结果大于6000,故C错误.


16. 新考法 结合新定义考查规律探究平面直角坐标系中,我们把横、纵坐标都是整数,且横、纵坐标之和大于0的点称为“和点”.将某“和点”平移,每次平移的方向取决于该点横、纵坐标之和除以3所得的余数(当余数为0时,向右平移;当余数为1时,向上平移;当余数为2时,向左平移),每次平移1个单位长度.
例:“和点”$P(2,1)$按上述规则连续平移3次后,到达点$P_{3}(2,2)$,其平移过程如下:$P(2,1)\xrightarrow[余0]{右}P_{1}(3,1)\xrightarrow[余1]{上}P_{2}(3,2)\xrightarrow[余2]{左}P_{3}(2,2)$.
若“和点”$Q$按上述规则连续平移16次后,到达点$Q_{16}(-1,9)$,则点$Q$的坐标为(
A.$(6,1)$或$(7,1)$
B.$(15,-7)$或$(8,0)$
C.$(6,0)$或$(8,0)$
D.$(5,1)$或$(7,1)$
例:“和点”$P(2,1)$按上述规则连续平移3次后,到达点$P_{3}(2,2)$,其平移过程如下:$P(2,1)\xrightarrow[余0]{右}P_{1}(3,1)\xrightarrow[余1]{上}P_{2}(3,2)\xrightarrow[余2]{左}P_{3}(2,2)$.
若“和点”$Q$按上述规则连续平移16次后,到达点$Q_{16}(-1,9)$,则点$Q$的坐标为(
D
)A.$(6,1)$或$(7,1)$
B.$(15,-7)$或$(8,0)$
C.$(6,0)$或$(8,0)$
D.$(5,1)$或$(7,1)$
答案:
16 D 当点$Q$的余数(“余数”指“横、纵坐标之和除以3所得的余数”)分别为0,1,2时,平移规律如下:
点Q的余数为 0时 点Q的余数为 1时 点Q的余数为 2时
平移规律
先向右平移1个单位长度,再向上、向左循环 向上、向左循环 向左、向上循环
由上可知,当点$Q$的余数为0时,连续平移16次后的余数为2;当点$Q$的余数为1时,连续平移16次后的余数为1;当点$Q$的余数为2时,连续平移16次后的余数为2.设$Q(m,n)$.$\because Q_{16}$的余数为2,$\therefore$分两种情况讨论.①当点$Q$的余数为0时,点$Q$向右平移1个单位长度后,得到点$Q_{1}(m + 1,n)$,结合平移规律知$Q_{16}$的坐标为$(m + 1 - 7,n + 8)$,即$(m - 6,n + 8)$,$\therefore m - 6 = - 1$,$n + 8 = 9$,解得$m = 5$,$n = 1$,$\therefore Q(5,1)$.②当点$Q$的余数为2时,$Q_{16}$的坐标为$(m - 8,n + 8)$,$\therefore m - 8 = - 1$,$n + 8 = 9$,解得$m = 7$,$n = 1$,$\therefore Q(7,1)$.故选D.
点Q的余数为 0时 点Q的余数为 1时 点Q的余数为 2时
平移规律
先向右平移1个单位长度,再向上、向左循环 向上、向左循环 向左、向上循环
由上可知,当点$Q$的余数为0时,连续平移16次后的余数为2;当点$Q$的余数为1时,连续平移16次后的余数为1;当点$Q$的余数为2时,连续平移16次后的余数为2.设$Q(m,n)$.$\because Q_{16}$的余数为2,$\therefore$分两种情况讨论.①当点$Q$的余数为0时,点$Q$向右平移1个单位长度后,得到点$Q_{1}(m + 1,n)$,结合平移规律知$Q_{16}$的坐标为$(m + 1 - 7,n + 8)$,即$(m - 6,n + 8)$,$\therefore m - 6 = - 1$,$n + 8 = 9$,解得$m = 5$,$n = 1$,$\therefore Q(5,1)$.②当点$Q$的余数为2时,$Q_{16}$的坐标为$(m - 8,n + 8)$,$\therefore m - 8 = - 1$,$n + 8 = 9$,解得$m = 7$,$n = 1$,$\therefore Q(7,1)$.故选D.
17. 某校生物小组的9名同学各用100粒种子做发芽实验,几天后观察并记录种子的发芽数分别为:89,73,90,86,75,86,89,95,89,以上数据的众数为
89
.
答案:
17 89
18. 已知$a$,$b$,$n$均为正整数.
(1)若$n < \sqrt{10} < n + 1$,则$n=$
(2)若$n - 1 < \sqrt{a} < n$,$n < \sqrt{b} < n + 1$,则满足条件的$a$的个数总比$b$的个数少
(1)若$n < \sqrt{10} < n + 1$,则$n=$
3
;(2)若$n - 1 < \sqrt{a} < n$,$n < \sqrt{b} < n + 1$,则满足条件的$a$的个数总比$b$的个数少
2
个.
答案:
18
(1)3
(2)2
【解析】
(1)$\because 9 < 10 < 16$,$\therefore 3 < \sqrt{10} < 4$,$\therefore n = 3$.
(2)$\because a$,$b,n$均为正整数,$\therefore n - 1,n,n + 1$为连续的三个自然数.$\because n - 1 < \sqrt{a} < n$,$n < \sqrt{b} < n + 1$,$\therefore (n - 1)^{2}< a < n^{2}$,$n^{2}< b < (n + 1)^{2}$,$\therefore$满足条件的$a$的个数为$n^{2}-(n - 1)^{2}-1 = 2n - 2$(点拨:可利用赋值法探究$a$的个数与$n$的关系,如当$n = 2$时,$1 < a < 4$,满足条件的$a$的个数是2,$2 = 4 - 1 - 1$),满足条件的$b$的个数为$(n + 1)^{2}-n^{2}-1 = 2n$,$\therefore$满足条件的$a$的个数总比$b$的个数少2个.
名师讲方法
解题步骤
二次根式估值的一般步骤
1.对二次根式平方;(以求$\sqrt{7}$的范围为例,$(\sqrt{7})^{2}=7$)
2.找出与平方后所得数字相邻的两个完全平方数;($4 < 7 < 9$)
3.对以上两个完全平方数开方;($\sqrt{4}=2$,$\sqrt{9}=3$)
4.确定这个二次根式的值的范围。($2 < \sqrt{7} < 3$)
若要求与该二次根式离得最近的整数(以求与$\sqrt{7}$最接近的整数为例),则需:
5.求以上两个整数的平均数;($ (2 + 3)÷ 2 = 2.5$)
6.比较二次根式和这个平均数的大小;($2.5^{2}=6.25 < 7$,所以$2.5 < \sqrt{7}$)
7.确定二次根式离哪个整数更近。(所以与$\sqrt{7}$最接近的整数是3)
(1)3
(2)2
【解析】
(1)$\because 9 < 10 < 16$,$\therefore 3 < \sqrt{10} < 4$,$\therefore n = 3$.
(2)$\because a$,$b,n$均为正整数,$\therefore n - 1,n,n + 1$为连续的三个自然数.$\because n - 1 < \sqrt{a} < n$,$n < \sqrt{b} < n + 1$,$\therefore (n - 1)^{2}< a < n^{2}$,$n^{2}< b < (n + 1)^{2}$,$\therefore$满足条件的$a$的个数为$n^{2}-(n - 1)^{2}-1 = 2n - 2$(点拨:可利用赋值法探究$a$的个数与$n$的关系,如当$n = 2$时,$1 < a < 4$,满足条件的$a$的个数是2,$2 = 4 - 1 - 1$),满足条件的$b$的个数为$(n + 1)^{2}-n^{2}-1 = 2n$,$\therefore$满足条件的$a$的个数总比$b$的个数少2个.
名师讲方法
解题步骤
二次根式估值的一般步骤
1.对二次根式平方;(以求$\sqrt{7}$的范围为例,$(\sqrt{7})^{2}=7$)
2.找出与平方后所得数字相邻的两个完全平方数;($4 < 7 < 9$)
3.对以上两个完全平方数开方;($\sqrt{4}=2$,$\sqrt{9}=3$)
4.确定这个二次根式的值的范围。($2 < \sqrt{7} < 3$)
若要求与该二次根式离得最近的整数(以求与$\sqrt{7}$最接近的整数为例),则需:
5.求以上两个整数的平均数;($ (2 + 3)÷ 2 = 2.5$)
6.比较二次根式和这个平均数的大小;($2.5^{2}=6.25 < 7$,所以$2.5 < \sqrt{7}$)
7.确定二次根式离哪个整数更近。(所以与$\sqrt{7}$最接近的整数是3)
19. 如图,$\triangle ABC$的面积为2,$AD$为$BC$边上的中线,点$A$,$C_{1}$,$C_{2}$,$C_{3}$是线段$CC_{4}$的五等分点,点$A$,$D_{1}$,$D_{2}$是线段$DD_{3}$的四等分点,点$A$是线段$BB_{1}$的中点.
(1)$\triangle AC_{1}D_{1}$的面积为
(2)$\triangle B_{1}C_{4}D_{3}$的面积为
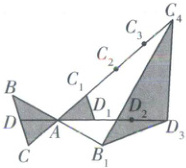
(1)$\triangle AC_{1}D_{1}$的面积为
1
;(2)$\triangle B_{1}C_{4}D_{3}$的面积为
7
.
答案:
19
(1)1
(2)7
【解析】
(1)$\because \triangle ABC$的面积为2,$AD$为$BC$边上的中线,$\therefore S_{\triangle ACD}=\frac{1}{2}S_{\triangle ABC}=1$.由题意知$AD = AD_{1}$,$AC = AC_{1}$.又$\because \angle CAD = \angle C_{1}AD$,$\therefore \triangle ACD\cong \triangle AC_{1}D(SAS)$,$\therefore S_{\triangle AC_{1}D}=S_{\triangle ACD}=1$.
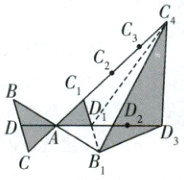
(2)如图,连接$B_{1}D_{1}$,同上易证$\triangle AB_{1}D_{1}\cong \triangle ABD$,$\therefore S_{\triangle AB_{1}D_{1}}=S_{\triangle ABD}=1$,$\angle B_{1}D_{1}A = \angle BDA$.又$\because \angle BDA + \angle CDA = 180^{\circ}$,$\angle CDA = \angle C_{1}D_{1}A$,$\therefore \angle B_{1}D_{1}A + \angle C_{1}D_{1}A = 180^{\circ}$,$\therefore C_{1}$,$D_{1}$,$B_{1}$三点共线,$\therefore S_{\triangle AB_{1}C_{1}}=1 + 1 = 2.\because AC_{4}=4AC_{1}$,$\therefore S_{\triangle AB_{1}C_{4}}=4S_{\triangle AB_{1}C_{1}}=8$.连接$D_{1}C_{4}$,则$S_{\triangle AD_{1}C_{4}}=4S_{\triangle AC_{1}D}=4$,$\therefore S_{\triangle AD_{1}C_{4}}=3S_{\triangle AB_{1}D_{1}}=3$,$\therefore S_{\triangle B_{1}C_{4}D_{1}}=S_{\triangle AD_{1}C_{4}}+S_{\triangle AB_{1}D_{1}}-S_{\triangle AB_{1}C_{1}}=12 + 3 - 8 = 7$.
名师讲方法
解题突破
解决第
(2)问的关键是利用直观想象,将$\triangle B_{1}C_{4}D_{1}$的面积转化为四边形$AB_{1}D_{1}C_{4}$与$\triangle AB_{1}C_{1}$的面积之差求解。本题已知多个等分点,故可将图形分割,求出相关三角形的面积。
19
(1)1
(2)7
【解析】
(1)$\because \triangle ABC$的面积为2,$AD$为$BC$边上的中线,$\therefore S_{\triangle ACD}=\frac{1}{2}S_{\triangle ABC}=1$.由题意知$AD = AD_{1}$,$AC = AC_{1}$.又$\because \angle CAD = \angle C_{1}AD$,$\therefore \triangle ACD\cong \triangle AC_{1}D(SAS)$,$\therefore S_{\triangle AC_{1}D}=S_{\triangle ACD}=1$.
(2)如图,连接$B_{1}D_{1}$,同上易证$\triangle AB_{1}D_{1}\cong \triangle ABD$,$\therefore S_{\triangle AB_{1}D_{1}}=S_{\triangle ABD}=1$,$\angle B_{1}D_{1}A = \angle BDA$.又$\because \angle BDA + \angle CDA = 180^{\circ}$,$\angle CDA = \angle C_{1}D_{1}A$,$\therefore \angle B_{1}D_{1}A + \angle C_{1}D_{1}A = 180^{\circ}$,$\therefore C_{1}$,$D_{1}$,$B_{1}$三点共线,$\therefore S_{\triangle AB_{1}C_{1}}=1 + 1 = 2.\because AC_{4}=4AC_{1}$,$\therefore S_{\triangle AB_{1}C_{4}}=4S_{\triangle AB_{1}C_{1}}=8$.连接$D_{1}C_{4}$,则$S_{\triangle AD_{1}C_{4}}=4S_{\triangle AC_{1}D}=4$,$\therefore S_{\triangle AD_{1}C_{4}}=3S_{\triangle AB_{1}D_{1}}=3$,$\therefore S_{\triangle B_{1}C_{4}D_{1}}=S_{\triangle AD_{1}C_{4}}+S_{\triangle AB_{1}D_{1}}-S_{\triangle AB_{1}C_{1}}=12 + 3 - 8 = 7$.

名师讲方法
解题突破
解决第
(2)问的关键是利用直观想象,将$\triangle B_{1}C_{4}D_{1}$的面积转化为四边形$AB_{1}D_{1}C_{4}$与$\triangle AB_{1}C_{1}$的面积之差求解。本题已知多个等分点,故可将图形分割,求出相关三角形的面积。
查看更多完整答案,请扫码查看


