《2026年金考卷中考45套汇编数学河北专版》

19. （本小题满分8分）
数学活动课上，刘老师让同学们做一个数学游戏，规则如下：每次游戏都涉及A，B，C三种运算，A，B，C代表的运算如图所示。每一种运算是在上一步运算结束后进行的一步运算。运算过程中自动添加必要的括号。例如：对数1按A→B→C的顺序运算，列式为[1 + (-3) - 6]×(-$\frac{1}{2}$)。

（1）求对数-4按A→B→C的顺序运算后的结果。
（2）对数a按A→C→B的顺序运算后，结果大于-6。请从下面的问题①和②中选择一个进行解答：
①直接写出a的正整数值；
②求a的取值范围。

答案： 19
(1)由题意，得$[-4 + (-3) - 6]×(-\frac{1}{2}) = (-13)×(-\frac{1}{2}) = \frac{13}{2}. (2)$由题意，得$[a + (-3)]×(-\frac{1}{2}) - 6 ＞ -6，$解得a ＜ 3. ①a的正整数值为1,2. ②a的取值范围为a ＜ 3.

20. （本小题满分8分）
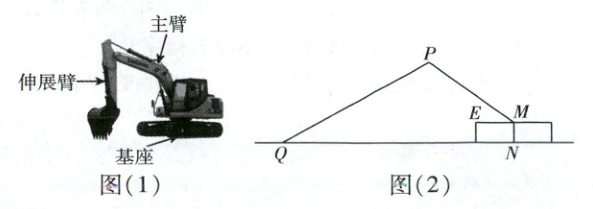
如图（1）是某型号挖掘机，该挖掘机是由基座、主臂和伸展臂构成。如图（2）是其在某种工作状态下的侧面结构示意图。已知EM//QN，基座高度MN为1 m，主臂MP的长为5 m，测得主臂伸展角∠PME = 37°。
（1）求点P到地面的高度；
（2）当挖掘机挖到地面上的点Q处时，∠MPQ = 113°，求QN的长。（结果保留根号）
（参考数据：sin37°取$\frac{3}{5}$，tan37°取$\frac{3}{4}$，sin53°取$\frac{4}{5}$，tan53°取$\frac{4}{3}$）

答案：
20
(1)如图，过点P作PH⊥QN于H，延长ME交PH于F，  

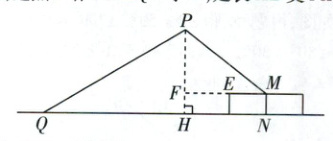
则四边形MNHF为矩形，
∴FH = MN = 1 m，∠PFM = 90°，
∴$PF = PM·sin∠PME = PM·sin37° ≈ 5×\frac{3}{5} = 3(m)，$
∴PH = PF + FH = 4 m. 答：点P到地面的高度为4 m.
(2)由
(1)可知，四边形MNHF为矩形，
∴$HN = FM = PM·cos∠PME = PM·cos37° ≈ 5×\frac{4}{5} = 4(m). $
∵∠PME = 37°，
∴∠MPF = 53°，
∴∠QPH = 113° - 53° = 60°.
∵PH = 4 m，
∴$tan∠QPH = \frac{QH}{PH} = \sqrt{3}，$
∴$QH = 4\sqrt{3} m，$
∴$QN = QH + HN = (4\sqrt{3} + 4)m.$