2026年金考卷中考45套汇编数学河北专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年金考卷中考45套汇编数学河北专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
20. (本小题满分8分)
某工厂生产A,B,C,D四种产品.为提升产品的竞争力,该工厂计划对部分种类的产品优化生产流程,降低成本;对其他种类的产品增加研发投入,提升品质.经研究,该工厂做出了甲、乙两种调整方案,这两种方案将对四种产品的成本产生不同的影响.
下面是该工厂这四种产品的部分信息:
a. 调整前,各产品年产量的不完整的条形统计图(图(1))和扇形统计图(图(2)).
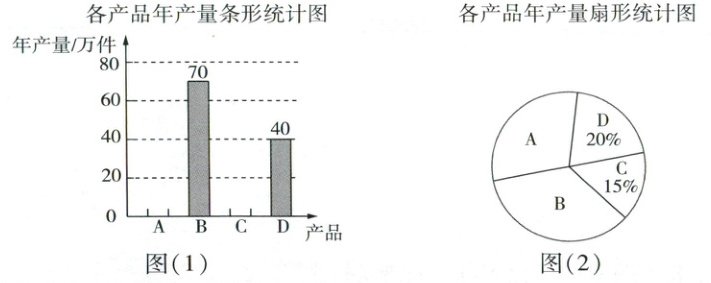
b. 各产品单件成本的核算情况统计表及说明.

说明:对于统计表中的数据,方案甲的平均数与调整前的相同,方案乙的中位数与调整前的相同.
根据以上信息,解答下列问题:
(1)求调整前A产品的年产量;
(2)直接写出m,n的值;
(3)若调整后这四种产品的年产量均与调整前的相同,请通过计算说明甲、乙两种方案哪种总成本较低.
某工厂生产A,B,C,D四种产品.为提升产品的竞争力,该工厂计划对部分种类的产品优化生产流程,降低成本;对其他种类的产品增加研发投入,提升品质.经研究,该工厂做出了甲、乙两种调整方案,这两种方案将对四种产品的成本产生不同的影响.
下面是该工厂这四种产品的部分信息:
a. 调整前,各产品年产量的不完整的条形统计图(图(1))和扇形统计图(图(2)).

b. 各产品单件成本的核算情况统计表及说明.

说明:对于统计表中的数据,方案甲的平均数与调整前的相同,方案乙的中位数与调整前的相同.
根据以上信息,解答下列问题:
(1)求调整前A产品的年产量;
(2)直接写出m,n的值;
(3)若调整后这四种产品的年产量均与调整前的相同,请通过计算说明甲、乙两种方案哪种总成本较低.
答案:
(1)调整前四种产品的年产量之和为 40÷20% = 200(万件),
∴调整前 C 产品的年产量为 200×15% = 30(万件),
∴调整前 A 产品的年产量为 200 - 70 - 30 - 40 = 60(万件).
(2) m = 25, n = 28.
解法提示:
∵方案甲的平均数与调整前的相同,
∴18 + 26 + 20 + 36 = 13 + 22 + 40 + m, 解得 m = 25.
∵方案乙的中位数与调整前的相同, 调整前的中位数为$\frac{20 + 26}{2}$ = 23(元),
∴$\frac{18 + n}{2}$ = 23(提示:已有的三个数据按从小到大的顺序排列为 16, 18, 32. 当中间两个数是 16, 18 时, 中位数是 17; 当中间两个数是 18, 32 时, 中位数是 25. 故当中间两个数是 18, n 时符合题意),
∴n = 28.
(3)方案甲年总成本与方案乙年总成本的差为(13 - 16)×60 + (22 - 28)×70 + (25 - 18)×30 + (40 - 32)×40 = -70 < 0,
∴方案甲总成本较低.
(1)调整前四种产品的年产量之和为 40÷20% = 200(万件),
∴调整前 C 产品的年产量为 200×15% = 30(万件),
∴调整前 A 产品的年产量为 200 - 70 - 30 - 40 = 60(万件).
(2) m = 25, n = 28.
解法提示:
∵方案甲的平均数与调整前的相同,
∴18 + 26 + 20 + 36 = 13 + 22 + 40 + m, 解得 m = 25.
∵方案乙的中位数与调整前的相同, 调整前的中位数为$\frac{20 + 26}{2}$ = 23(元),
∴$\frac{18 + n}{2}$ = 23(提示:已有的三个数据按从小到大的顺序排列为 16, 18, 32. 当中间两个数是 16, 18 时, 中位数是 17; 当中间两个数是 18, 32 时, 中位数是 25. 故当中间两个数是 18, n 时符合题意),
∴n = 28.
(3)方案甲年总成本与方案乙年总成本的差为(13 - 16)×60 + (22 - 28)×70 + (25 - 18)×30 + (40 - 32)×40 = -70 < 0,
∴方案甲总成本较低.
21. (本小题满分9分)
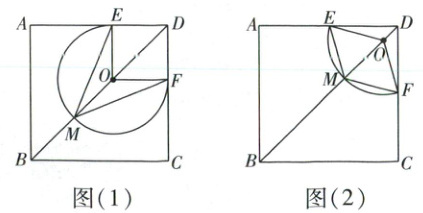
如图(1),图(2),正方形ABCD的边长为5.扇形OEF所在圆的圆心O在对角线BD上,且不与点D重合,半径OE=2,点E,F分别在边AD,CD上,DE=DF(DE≥2),扇形OEF的弧交线段OB于点M,记为$\overset{\frown}{EMF}$.
(1)如图(1),当AE=3时,求∠EMF的度数;
(2)如图(2),当四边形OEMF为菱形时,求DE的长;
(3)当∠EOF=150°时,求$\overset{\frown}{EMF}$的长.
如图(1),图(2),正方形ABCD的边长为5.扇形OEF所在圆的圆心O在对角线BD上,且不与点D重合,半径OE=2,点E,F分别在边AD,CD上,DE=DF(DE≥2),扇形OEF的弧交线段OB于点M,记为$\overset{\frown}{EMF}$.
(1)如图(1),当AE=3时,求∠EMF的度数;
(2)如图(2),当四边形OEMF为菱形时,求DE的长;
(3)当∠EOF=150°时,求$\overset{\frown}{EMF}$的长.

答案:
(1)
∵AD = 5, AE = 3,
∴DF = DE = 5 - 3 = 2.
又
∵OE = OF = 2,
∴DE = DF = OE = OF,
∴四边形 DEOF 是菱形.
∵四边形 ABCD 是正方形,
∴∠ADC = 90°,
∴∠EOF = 90°(依据:圆周角定理),
∴∠EMF = $\frac{1}{2}$∠EOF = 45°.
(2)
∵四边形 OEMF 为菱形,
∴EM = OE.
又
∵OE = OM,
∴EM = OE = OM,
∴△OEM 是等边三角形,
∴∠EOM = 60°.
如图
(1), 过点 E 作 EG⊥DM 于点 G.

巧作辅助线:欲求 DE 的长, 构造其所在的 Rt△DEG
在 Rt△EOG 中, EG = OE·sin60° = $\sqrt{3}$.
在 Rt△DEG 中, DE = $\frac{EG}{sin45°}$ = $\sqrt{6}$.
(3)当$\overset{\frown}{EMF}$是劣弧时, 如图
(2), EMF 的长为$\frac{150\pi×2}{180}$ = $\frac{5\pi}{3}$.
当$\overset{\frown}{EMF}$是优弧时, 如图
(3).
∵∠EOF = 150°,
∴$\overset{\frown}{EMF}$所对的圆心角为 360° - 150° = 210°,
∴$\overset{\frown}{EMF}$的长为$\frac{210\pi×2}{180}$ = $\frac{7\pi}{3}$.
综上所述, $\overset{\frown}{EMF}$的长为$\frac{5\pi}{3}$或$\frac{7\pi}{3}$.


(1)
∵AD = 5, AE = 3,
∴DF = DE = 5 - 3 = 2.
又
∵OE = OF = 2,
∴DE = DF = OE = OF,
∴四边形 DEOF 是菱形.
∵四边形 ABCD 是正方形,
∴∠ADC = 90°,
∴∠EOF = 90°(依据:圆周角定理),
∴∠EMF = $\frac{1}{2}$∠EOF = 45°.
(2)
∵四边形 OEMF 为菱形,
∴EM = OE.
又
∵OE = OM,
∴EM = OE = OM,
∴△OEM 是等边三角形,
∴∠EOM = 60°.
如图
(1), 过点 E 作 EG⊥DM 于点 G.

巧作辅助线:欲求 DE 的长, 构造其所在的 Rt△DEG
在 Rt△EOG 中, EG = OE·sin60° = $\sqrt{3}$.
在 Rt△DEG 中, DE = $\frac{EG}{sin45°}$ = $\sqrt{6}$.
(3)当$\overset{\frown}{EMF}$是劣弧时, 如图
(2), EMF 的长为$\frac{150\pi×2}{180}$ = $\frac{5\pi}{3}$.
当$\overset{\frown}{EMF}$是优弧时, 如图
(3).
∵∠EOF = 150°,
∴$\overset{\frown}{EMF}$所对的圆心角为 360° - 150° = 210°,
∴$\overset{\frown}{EMF}$的长为$\frac{210\pi×2}{180}$ = $\frac{7\pi}{3}$.
综上所述, $\overset{\frown}{EMF}$的长为$\frac{5\pi}{3}$或$\frac{7\pi}{3}$.


查看更多完整答案,请扫码查看


