2026年金考卷中考45套汇编数学河北专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年金考卷中考45套汇编数学河北专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第30页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
25. (本小题满分10分)
如图是某同学正在设计的一动画示意图,x轴上依次有A,O,N三个点,且$AO = 2$,在ON上方有五个台阶$T_{1} \sim T_{5}$(各拐角均为$90^{\circ}$),每个台阶的高、宽分别是1和1.5,台阶$T_{1}$到x轴的距离$OK = 10$.从点A处向右上方沿抛物线$L:y = -x^{2} + 4x + 12$发出一个带光的点P.
(1) 求点A的横坐标,在图中补画出y轴,并
(2) 当点P落到台阶上后立即弹起,又形成了另一条与L形状相同的抛物线C,且最大高度为11,求C的解析式,并说明其对称轴是否与台阶$T_{5}$有交点.
(3) 在x轴上从左到右有两点D,E,且$DE = 1$,从点E向上作$EB \perp x$轴,且$BE = 2$.在$\triangle BDE$沿x轴左右平移时,必须保证(2)中沿抛物线C下落的点P能落在边BD(包括端点)上,则点B横坐标的最大值比最小值大多少?
【注:(2)中不必写x的取值范围】

如图是某同学正在设计的一动画示意图,x轴上依次有A,O,N三个点,且$AO = 2$,在ON上方有五个台阶$T_{1} \sim T_{5}$(各拐角均为$90^{\circ}$),每个台阶的高、宽分别是1和1.5,台阶$T_{1}$到x轴的距离$OK = 10$.从点A处向右上方沿抛物线$L:y = -x^{2} + 4x + 12$发出一个带光的点P.
(1) 求点A的横坐标,在图中补画出y轴,并
直
接
指出点P会落在哪个台阶上.(2) 当点P落到台阶上后立即弹起,又形成了另一条与L形状相同的抛物线C,且最大高度为11,求C的解析式,并说明其对称轴是否与台阶$T_{5}$有交点.
(3) 在x轴上从左到右有两点D,E,且$DE = 1$,从点E向上作$EB \perp x$轴,且$BE = 2$.在$\triangle BDE$沿x轴左右平移时,必须保证(2)中沿抛物线C下落的点P能落在边BD(包括端点)上,则点B横坐标的最大值比最小值大多少?
【注:(2)中不必写x的取值范围】

答案:
25

(1)当$y = 0$时,$-x^{2}+4x + 12 = 0$,解得$x_{1}=-2$,$x_{2}=6$,
由题意知点A为L与$x$轴的左交点,
∴点A的横坐标为$-2$.
y轴如图.
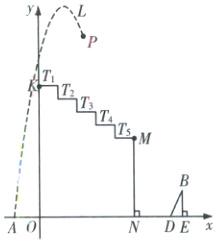
点P会落在台阶$T_4$上.
(2)由题意,设抛物线C的解析式为$y = -(x - h)^{2}+11$.
计算易得点P落在$T$上的点$(5,7)$处,
把$x = 5$,$y = 7$代入$y = -(x - h)^{2}+11$,
得$7 = -(5 - h)^{2}+11$,
解得$h_{1}=7$,$h_{2}=3$,
由题意可知$h>5$,
∴$h = 7$,
∴抛物线C的解析式为$y = -(x - 7)^{2}+11$.
易知抛物线C的对称轴为直线$x = 7$,
∵$6<7<7.5$,
∴该对称轴与台阶$T$有交点.
(3)由
(2)知当点P落在B,D处时,其横坐标$x>7$,
对于$y = -(x - 7)^{2}+11$,
当$y = 2$时,$2 = -(x - 7)^{2}+11$,解得$x_{1}=10$,$x_{2}=4$,
∴点P落在点B处时,$x_{B}=10$;
当$y = 0$时,$0 = -(x - 7)^{2}+11$,解得$x_{1}=7+\sqrt{11}$,$x_{2}=7-\sqrt{11}$,
∴点P落在点D处时,$x_{D}=7+\sqrt{11}$.
∴点B横坐标的最大值比最小值大$(7+\sqrt{11}+1)-10=\sqrt{11}-2$.
25

(1)当$y = 0$时,$-x^{2}+4x + 12 = 0$,解得$x_{1}=-2$,$x_{2}=6$,
由题意知点A为L与$x$轴的左交点,
∴点A的横坐标为$-2$.
y轴如图.

点P会落在台阶$T_4$上.
(2)由题意,设抛物线C的解析式为$y = -(x - h)^{2}+11$.
计算易得点P落在$T$上的点$(5,7)$处,
把$x = 5$,$y = 7$代入$y = -(x - h)^{2}+11$,
得$7 = -(5 - h)^{2}+11$,
解得$h_{1}=7$,$h_{2}=3$,
由题意可知$h>5$,
∴$h = 7$,
∴抛物线C的解析式为$y = -(x - 7)^{2}+11$.
易知抛物线C的对称轴为直线$x = 7$,
∵$6<7<7.5$,
∴该对称轴与台阶$T$有交点.
(3)由
(2)知当点P落在B,D处时,其横坐标$x>7$,
对于$y = -(x - 7)^{2}+11$,
当$y = 2$时,$2 = -(x - 7)^{2}+11$,解得$x_{1}=10$,$x_{2}=4$,
∴点P落在点B处时,$x_{B}=10$;
当$y = 0$时,$0 = -(x - 7)^{2}+11$,解得$x_{1}=7+\sqrt{11}$,$x_{2}=7-\sqrt{11}$,
∴点P落在点D处时,$x_{D}=7+\sqrt{11}$.
∴点B横坐标的最大值比最小值大$(7+\sqrt{11}+1)-10=\sqrt{11}-2$.
26. (本小题满分12分)
在一平面内,线段$AB = 20$,线段$BC = CD = DA = 10$,将这四条线段顺次首尾相接.把AB固定,让AD绕点A从AB开始逆时针旋转$\alpha(\alpha > 0^{\circ})$到某一位置时,BC,CD将会跟随出现到相应的位置.
论证 如图(1),当$AD // BC$时,设AB与CD交于点O,求证:$AO = 10$.
发现 当旋转角$\alpha = 60^{\circ}$时,$\angle ADC$的度数可能是多少?
尝试 取线段CD的中点M,当点M与点B距离最大时,求点M到AB的距离.
拓展 ①如图(2),设点D与B的距离为d,若$\angle BCD$的平分线所在直线交AB于点P,直
②当点C在AB下方,且AD与CD垂直时,直

在一平面内,线段$AB = 20$,线段$BC = CD = DA = 10$,将这四条线段顺次首尾相接.把AB固定,让AD绕点A从AB开始逆时针旋转$\alpha(\alpha > 0^{\circ})$到某一位置时,BC,CD将会跟随出现到相应的位置.
论证 如图(1),当$AD // BC$时,设AB与CD交于点O,求证:$AO = 10$.
发现 当旋转角$\alpha = 60^{\circ}$时,$\angle ADC$的度数可能是多少?
尝试 取线段CD的中点M,当点M与点B距离最大时,求点M到AB的距离.
拓展 ①如图(2),设点D与B的距离为d,若$\angle BCD$的平分线所在直线交AB于点P,直
接
写出BP的长(用含d的式子表示);②当点C在AB下方,且AD与CD垂直时,直
接
写出α的余弦值.
答案:
26 论证 证明:如图
(1),
∵$AD// BC$,
∴$\angle A = \angle B$,$\angle D = \angle C$.
又$AD = BC$,
∴$\triangle AOD≌\triangle BOC$,
∴$AO = BO=\frac{1}{2}AB = 10$.

发现 当$\alpha = 60^{\circ}$时,对点C的位置可分以下2种情况讨论:
①如图
(2),当A,B,C三点共线时,有$\triangle ADC$是等边三角形,
此时$\angle ADC = 60^{\circ}$.
②如图
(3),当A,B,C三点不共线时,
取AB的中点O,连接OD,
有$AD = AO = OD = BO = BC = CD = 10$,
即四边形BCDO为菱形,从而可得$CD// AB$,
∴$\angle ADC = 180^{\circ}-60^{\circ}=120^{\circ}$.
综上,$\angle ADC$可能是$60^{\circ}$或$120^{\circ}$.


尝试 连接BM,易知$BM\leq BC + CM$,
∴当B,C,D三点共线时,BM的长最大,如图
(4),
此时$BM = 15$.
作$DH\perp AB$,$MN\perp AB$,$BG\perp AD$,垂足分别是点H,N,G.
∵$BD = BC + CD = 20 = AB$,
∴$AG = GD=\frac{1}{2}AD = 5$,
∴$BG=\sqrt{AB^{2}-AG^{2}}=5\sqrt{15}$.
由$S_{\triangle ABD}=\frac{1}{2}AD· BG=\frac{1}{2}AB· DH$,
得$DH=\frac{AD· BG}{AB}=\frac{5\sqrt{15}}{2}$,
易证$Rt\triangle BMN∽Rt\triangle BDH$,
∴$\frac{BM}{BD}=\frac{MN}{DH}$,即$\frac{15}{20}=\frac{MN}{\frac{5\sqrt{15}}{2}}$,
∴$MN=\frac{15\sqrt{15}}{8}$,
即点M与点B距离最大时,点M到AB的距离为$\frac{15\sqrt{15}}{8}$.
拓展 ①$BP=\frac{20d^{2}}{d^{2}+300}$
②$\frac{5+\sqrt{7}}{8}$
解法提示:①如图
(5),连接BD交PC于点E,过点D作$DF\perp AB$于点F.
设$BF = x$,则$AF = 20 - x$.
∵$AD^{2}-AF^{2}=BD^{2}-BF^{2}$,
∴$10^{2}-(20 - x)^{2}=d^{2}-x^{2}$,解得$x=\frac{d^{2}+300}{40}$,
∵$CD = BC$,$CP$平分$\angle BCD$,
∴$CE\perp BD$,$BE = DE=\frac{1}{2}BD=\frac{d}{2}$,
∴$\angle PEB=\angle BFD = 90^{\circ}$.
又
∵$\angle PBE=\angle DBF$,
∴$\triangle BPE∽\triangle BDF$,
∴$\frac{BP}{BD}=\frac{BE}{BF}$,即$BP = d×\frac{\frac{d}{2}}{\frac{d^{2}+300}{40}}=\frac{20d^{2}}{d^{2}+300}$


②如图
(6),设AB交CD于点S,连接AC,过点C作$CR\perp AB$于点R,过点S作$ST\perp AC$于点T.
∵$\angle ADC = 90^{\circ}$,$AD = CD = 10$,
∴$AC = 10\sqrt{2}$.
设$AR = m$,则$BR = 20 - m$.
∵$AC^{2}-AR^{2}=BC^{2}-BR^{2}$,
∴$(10\sqrt{2})^{2}-m^{2}=10^{2}-(20 - m)^{2}$,解得$m=\frac{25}{2}$,
∴$CR=\sqrt{AC^{2}-AR^{2}}=\frac{5\sqrt{7}}{2}$,
∴$\tan\angle RAC=\frac{CR}{AR}=\frac{\sqrt{7}}{5}$,即$\frac{ST}{AT}=\frac{\sqrt{7}}{5}$.
设$AT = 5t$,则$TC = ST=\sqrt{7}t$,
∴$AS = 4\sqrt{2}t$,$5t+\sqrt{7}t = 10\sqrt{2}$,解得$t=\frac{10\sqrt{2}}{5+\sqrt{7}}$,
∴$AS = 4\sqrt{2}×\frac{10\sqrt{2}}{5+\sqrt{7}}=\frac{80}{5+\sqrt{7}}$,
∴$\cos\alpha=\frac{AD}{AS}=\frac{5+\sqrt{7}}{8}$.
26 论证 证明:如图
(1),
∵$AD// BC$,
∴$\angle A = \angle B$,$\angle D = \angle C$.
又$AD = BC$,
∴$\triangle AOD≌\triangle BOC$,
∴$AO = BO=\frac{1}{2}AB = 10$.

发现 当$\alpha = 60^{\circ}$时,对点C的位置可分以下2种情况讨论:
①如图
(2),当A,B,C三点共线时,有$\triangle ADC$是等边三角形,
此时$\angle ADC = 60^{\circ}$.
②如图
(3),当A,B,C三点不共线时,
取AB的中点O,连接OD,
有$AD = AO = OD = BO = BC = CD = 10$,
即四边形BCDO为菱形,从而可得$CD// AB$,
∴$\angle ADC = 180^{\circ}-60^{\circ}=120^{\circ}$.
综上,$\angle ADC$可能是$60^{\circ}$或$120^{\circ}$.


尝试 连接BM,易知$BM\leq BC + CM$,
∴当B,C,D三点共线时,BM的长最大,如图
(4),
此时$BM = 15$.
作$DH\perp AB$,$MN\perp AB$,$BG\perp AD$,垂足分别是点H,N,G.
∵$BD = BC + CD = 20 = AB$,
∴$AG = GD=\frac{1}{2}AD = 5$,
∴$BG=\sqrt{AB^{2}-AG^{2}}=5\sqrt{15}$.
由$S_{\triangle ABD}=\frac{1}{2}AD· BG=\frac{1}{2}AB· DH$,
得$DH=\frac{AD· BG}{AB}=\frac{5\sqrt{15}}{2}$,
易证$Rt\triangle BMN∽Rt\triangle BDH$,
∴$\frac{BM}{BD}=\frac{MN}{DH}$,即$\frac{15}{20}=\frac{MN}{\frac{5\sqrt{15}}{2}}$,
∴$MN=\frac{15\sqrt{15}}{8}$,
即点M与点B距离最大时,点M到AB的距离为$\frac{15\sqrt{15}}{8}$.
拓展 ①$BP=\frac{20d^{2}}{d^{2}+300}$
②$\frac{5+\sqrt{7}}{8}$
解法提示:①如图
(5),连接BD交PC于点E,过点D作$DF\perp AB$于点F.
设$BF = x$,则$AF = 20 - x$.
∵$AD^{2}-AF^{2}=BD^{2}-BF^{2}$,
∴$10^{2}-(20 - x)^{2}=d^{2}-x^{2}$,解得$x=\frac{d^{2}+300}{40}$,
∵$CD = BC$,$CP$平分$\angle BCD$,
∴$CE\perp BD$,$BE = DE=\frac{1}{2}BD=\frac{d}{2}$,
∴$\angle PEB=\angle BFD = 90^{\circ}$.
又
∵$\angle PBE=\angle DBF$,
∴$\triangle BPE∽\triangle BDF$,
∴$\frac{BP}{BD}=\frac{BE}{BF}$,即$BP = d×\frac{\frac{d}{2}}{\frac{d^{2}+300}{40}}=\frac{20d^{2}}{d^{2}+300}$


②如图
(6),设AB交CD于点S,连接AC,过点C作$CR\perp AB$于点R,过点S作$ST\perp AC$于点T.
∵$\angle ADC = 90^{\circ}$,$AD = CD = 10$,
∴$AC = 10\sqrt{2}$.
设$AR = m$,则$BR = 20 - m$.
∵$AC^{2}-AR^{2}=BC^{2}-BR^{2}$,
∴$(10\sqrt{2})^{2}-m^{2}=10^{2}-(20 - m)^{2}$,解得$m=\frac{25}{2}$,
∴$CR=\sqrt{AC^{2}-AR^{2}}=\frac{5\sqrt{7}}{2}$,
∴$\tan\angle RAC=\frac{CR}{AR}=\frac{\sqrt{7}}{5}$,即$\frac{ST}{AT}=\frac{\sqrt{7}}{5}$.
设$AT = 5t$,则$TC = ST=\sqrt{7}t$,
∴$AS = 4\sqrt{2}t$,$5t+\sqrt{7}t = 10\sqrt{2}$,解得$t=\frac{10\sqrt{2}}{5+\sqrt{7}}$,
∴$AS = 4\sqrt{2}×\frac{10\sqrt{2}}{5+\sqrt{7}}=\frac{80}{5+\sqrt{7}}$,
∴$\cos\alpha=\frac{AD}{AS}=\frac{5+\sqrt{7}}{8}$.
查看更多完整答案,请扫码查看


