《2026年金考卷中考45套汇编数学河北专版》

23. （本小题满分11分）
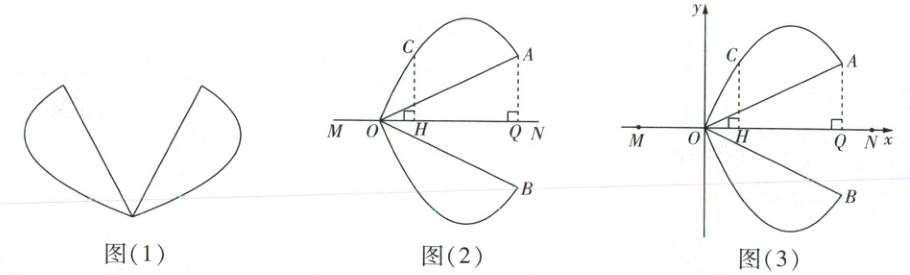
新素材 “花瓣”形工艺品 琪琪在学习二次函数之后，想用二次函数的知识解决生活中的实际问题. 她观察发现，家中有一款铁艺工艺品（厚度忽略不计），它由两个成轴对称的“花瓣”构成，图(1)是该工艺品的平面示意图，“花瓣”外边缘可以近似地看成抛物线形，内边缘是线段. 如图(2)，两个“花瓣”的公共顶点为O，对称轴为直线MN，内边缘为线段OA，OB，琪琪测得外边缘上一点C与O点的水平距离为1 dm（$OH = 1\ dm$）时，C点到对称轴MN的距离为2 dm（$CH = 2\ dm$），A点与O点的水平距离为4 dm（$OQ = 4\ dm$），A点到对称轴MN的距离为2 dm（$AQ = 2\ dm$）.
（1）如图(3)，以O为原点，以直线MN为x轴，建立平面直角坐标系.
①求出对称轴MN上方抛物线$C_{1}$的解析式；
②点E在抛物线$C_{1}$上，且点E到对称轴MN的距离最大，求点E的坐标.
（2）如图(3)，琪琪想在工艺品上安装4条竖直的铁丝，每条铁丝的两端分别固定在同一花瓣的内、外边缘上，且使得安装后的工艺品仍然关于直线MN对称. 琪琪说：总长10 dm的铁丝一定够用（不考虑损耗）. 你认为琪琪的说法对吗？并说明理由.
（3）琪琪想：若把这个“花瓣”形工艺品平放在一个正方形的托盘中，这个正方形托盘边长的最小值是多少呢？请直接写出这个最小值.

答案：
23
(1)①
∵ 抛物线C₁过点(0,0)，
∴ 设抛物线C₁的解析式为y = ax² + bx.
由题意得A(4,2)，C(1,2).
∵ 抛物线C₁过点A(4,2)，C(1,2)，
∴ $\begin{cases} 2 = 16a + 4b \\ 2 = a + b \end{cases}$，解得$\begin{cases} a = -\frac{1}{2} \\ b = \frac{5}{2} \end{cases}$，
∴ 抛物线C₁的解析式为y = -$\frac{1}{2}$x² + $\frac{5}{2}$x.
②
∵ y = -$\frac{1}{2}$x² + $\frac{5}{2}$x = -$\frac{1}{2}$(x - $\frac{5}{2}$)² + $\frac{25}{8}$，
∴ E点坐标为($\frac{5}{2}$,$\frac{25}{8}$).
(2)琪琪的说法对.理由如下：
设直线OA的解析式为y = kx.
∵ 直线OA过点A(4,2)，
∴ 2 = 4k，解得k = $\frac{1}{2}$，
∴ 直线OA的解析式为y = $\frac{1}{2}$x.
令z = -$\frac{1}{2}$x² + $\frac{5}{2}$x - $\frac{1}{2}$x = -$\frac{1}{2}$x² + 2x = -$\frac{1}{2}$(x - 2)² + 2，
则当x = 2时，z取最大值2，
∴ 在同一花瓣的内、外边缘上安装的竖直铁丝的最大长度是2 dm，
∴ 安装4条竖直的铁丝总长度小于10 dm，
∴ 总长10 cm的铁丝一定够用，
∴ 琪琪的说法对.
(3)$\frac{29\sqrt{2}}{8}$ dm.
解法提示：如图，正方形PGDR的每条边与“花瓣”形工艺品有且只有一个公共点，易知正方形PGDR的边长即为正方形托盘边长的最小值 (关键点1：将问题转化为求正方形PGDR的边长).

∵ 四边形PGDR为正方形，
∴ ∠ P = 90°，PG = PR，∠ PGR = 45°.
又
∵ ∠ GOF = 90°，
∴ OG = OF.
设OG = OF = n，则G(-n,0)，F(0,n).
设直线GF的解析式为y = mx + n (n ≠ 0).
把G(-n,0)代入，得0 = -mn + n，解得m = 1，
∴ 直线GF的解析式为y = x + n.
∵ 直线GF与抛物线C₁只有一个公共点，
∴ -$\frac{1}{2}$x² + $\frac{5}{2}$x = x + n，即x² - 3x + 2n = 0有两个相等的实数根，
∴ Δ = 0，即(-3)² - 4 × 1 × 2n = 0，解得n = $\frac{9}{8}$，
∴ 直线GF的解析式为y = x + $\frac{9}{8}$ (关键点2：根据OG = OF及直线GF与抛物线C₁只有一个公共点，求出直线GF的解析式).
当y = 0时，x = -$\frac{9}{8}$，
∴ G(-$\frac{9}{8}$,0) (关键点3：求出点G的坐标).
由
(1)知，抛物线C₁的顶点坐标为($\frac{5}{2}$,$\frac{25}{8}$)，
∴ 抛物线C₁的对称轴为直线x = $\frac{5}{2}$.
由对称性可知正方形PGDR的顶点R的坐标为($\frac{49}{8}$,0) (关键点4：求出点R的坐标)，
∴ GR = $\frac{49}{8}$ - (-$\frac{9}{8}$) = $\frac{29}{4}$，
∴ PG = $\frac{29}{4}$ × cos 45° = $\frac{29}{4}$ × $\frac{\sqrt{2}}{2}$ = $\frac{29\sqrt{2}}{8}$，
∴ 这个正方形托盘边长的最小值是$\frac{29\sqrt{2}}{8}$dm.

24. （本小题满分12分）
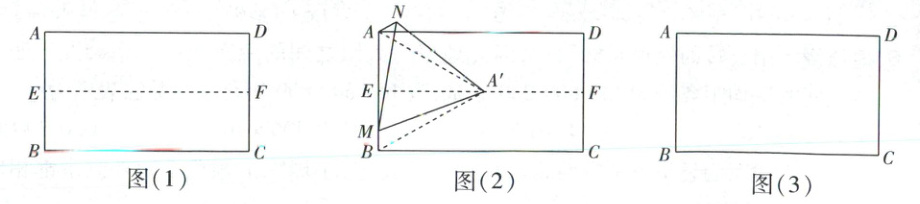
新考法 融入尺规作图 如图(1)，有一张矩形纸片ABCD，$AB = 6$，$AD = 10$. 将纸片进行两次折叠，第一次折叠使得点A与点B重合，得到折痕EF；第二次经过点B折叠，使点A的对称点$A'$落在EF上，得到折痕BG，G为折痕与AD的交点.
（1）尺规作图：在图(1)中作出点$A'$及折痕BG（借助无刻度的直尺和圆规，不写作法，保留作图痕迹）.
（2）连接$AA'$，$A'B$，判断$\triangle ABA'$的形状，并证明.
（3）如图(2)，在AB上取一点M，连接$A'M$，以$A'M$为边，在$A'M$上方作等边三角形$A'MN$，连接AN.
①若$BM = 1$，求$\tan\angle AMN$的值；
②连接CN，直接写出CN的最小值.
（4）如何折出一个面积最大的等边三角形？在图(3)中画出折痕并简要说明折法.

答案：
24
(1)作图如图
(1)所示 (作法不唯一).

(2)△ ABA'是等边三角形.
证明：由折叠可知AA' = A'B，A'B = AB，
∴ AA' = A'B = AB，
∴ △ ABA'是等边三角形.
(3)①
∵ △ A'MN，△ ABA'都是等边三角形，
∴ ∠ ABA' = ∠ A'MN = 60°，
∴ ∠ AMN + ∠ A'MB = ∠ A'MB + ∠ BA'M = 120°，
∴ ∠ AMN = ∠ BA'M (关键点：转化角，从而将求tan ∠ AMN转化为求tan ∠ BA'M).
如图
(2)，过点M作MH ⊥ A'B于点H，则∠ BHM = ∠ A'HM = 90°.

∵ △ ABA'是等边三角形，
∴ A'B = AB = 6.
在Rt△ BMH中，BM = 1，
∴ BH = BM · cos 60° = $\frac{1}{2}$，MH = BM · sin 60° = $\frac{\sqrt{3}}{2}$，
∴ A'H = A'B - BH = $\frac{11}{2}$，
∴ tan ∠ BA'M = $\frac{MH}{A'H}$ = $\frac{\sqrt{3}}{11}$，
∴ tan ∠ AMN = $\frac{\sqrt{3}}{11}$
② 3$\sqrt{3}$ + 5.
快招解题法 试题秒解 考场速用
本问可利用“手拉手”模型求出∠ NAA' = 60°，即得到点N在定直线上运动，再利用“垂线段最短”确定出CN最短时点N的位置，再求解即可.解法提示如下：
∵ △ A'MN，△ ABA'都是等边三角形，
∴ ∠ BA'A = ∠ MA'N = 60°，AA' = BA'，A'N = MA'，
∴ ∠ BA'M = 60° - ∠ AA'M = ∠ AA'N，
∴ △ BA'M ≌ △ AA'N (点拨：“手拉手”模型)，
∴ ∠ NAA' = ∠ A'BM = 60° (关键点1：判断出点N在定直线上运动).
易得∠ A'AD = 90° - ∠ BAA' = 90° - 60° = 30°，
∴ ∠ NAD = 60° - ∠ A'AD = 30° (关键点2：判断出∠ NAD = 30°).
易知当CN ⊥ AN时，CN的长度最短 (点拨：根据“垂线段最短”)，如图
(3)，设CN与AD交于点Q，

则∠ CQD = ∠ AQN = 90° - 30° = 60°.
易得CQ = $\frac{CD}{\sin 60°}$ = 4$\sqrt{3}$，DQ = 2$\sqrt{3}$，
∴ AQ = AD - DQ = 10 - 2$\sqrt{3}$，
∴ NQ = $\frac{1}{2}$AQ = 5 - $\sqrt{3}$，
∴ CN = CQ + NQ = 4$\sqrt{3}$ + 5 - $\sqrt{3}$ = 3$\sqrt{3}$ + 5.
故CN的最小值为3$\sqrt{3}$ + 5.
(4)如图
(4)，
①将纸片折叠，使得点A与点B重合，得到折痕EF；
②经过点B折叠，使点A的对称点A'落在EF上，得到折痕BG；
③沿点B，A'所在的直线折叠，点G的对称点M落在BC边上，得到折痕BP.
△ BGM即为所求的面积最大的等边三角形.