《2026年金考卷中考45套汇编数学河北专版》

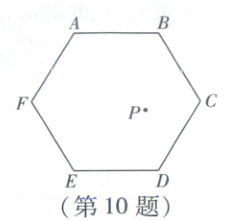
10. 如图，点$P$是正六边形$ABCDEF$内部一个动点，$AB = 1\mathrm{cm}$，则点$P$到这个正六边形六条边的距离之和为(C)

A.$6\mathrm{cm}$
B.$3\mathrm{cm}$
C.$3\sqrt{3}\mathrm{cm}$
D.$6\sqrt{3}\mathrm{cm}$

答案：
10C 如图，过点P作PM⊥AB于点M，延长MP交ED于点N。易证正六边形的对边平行，
∴PN⊥DE。设正六边形ABCDEF的中心为O，过点O作OG⊥AB于点G，延长GO交ED于点H，则MN = GH = 2OG（点拨：①平行线间的距离处处相等；②正六边形的中心到其各边的距离相等）。易知点P到正六边形六条边的距离之和为6OG（关键点）。
∵OA = OB，∠AOB = 360°÷6 = 60°，
∴△AOB是等边三角形，
∴∠OAG = 60°，AG = $\frac{1}{2}$AB = $\frac{1}{2}$cm，
∴OG = $\sqrt{3}$AG = $\frac{\sqrt{3}}{2}$cm，
∴点P到这个正六边形六条边的距离之和为6×$\frac{\sqrt{3}}{2} = 3\sqrt{3}$cm。

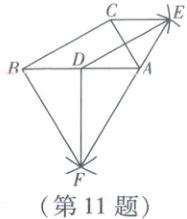
11. 如图，在$\mathrm{Rt}\triangle ABC$中，$\angle ACB = 90^{\circ}$，$\angle ABC = 30^{\circ}$，$D$为$AB$的中点。分别以点$A$，$C$为圆心，$AC$长为半径画弧，两弧交于点$E$；分别以点$A$，$B$为圆心，$AB$长为半径画弧，两弧交于点$F$。连接$DE$，$DF$。有以下4个结论：①$F$，$A$，$E$三点共线；②四边形$BDEC$为平行四边形；③$AC\perp DE$；④$S_{\triangle ACE}:S_{四边形BCEF} = 1:6$。其中正确的是(B)

A.只有①②
B.只有①②③
C.只有③④
D.①②③④

答案： 11B 分析如下，可知正确的是①②③。
序号 分析 正误
① 易知∠BAC = 90° - 30° = 60°。由作图可知△ACE，△ABF均为等边三角形，
∴∠CAE = ∠BAF = 60°，
∴∠FAE = 3×60° = 180°，
∴F，A，E三点共线（点拨：证明角度和为180°是证明共线的常用方法）。 √
②
∵∠ACB = 90°，∠B = 30°，
∴AB = 2AC。又
∵点D为AB的中点，
∴BD = AC = CE。
∵∠BAC = ∠ACE = 60°，
∴AB//CE，
∴四边形BDEC是平行四边形（依据：有一组对边平行且相等的四边形是平行四边形）。 √
③ 由②可知四边形BDEC是平行四边形，BC//DE。又
∵∠ACB = 90°，
∴AC⊥DE。
∵CE//AB，AB = 2AC = 2CE，
∴$S_{△ABC} = 2S_{△ACE}$（点拨：等高三角形的面积之比等于底之比）。 √
④ 易知△ACE∽△ABF，
∴$\frac{S_{△ACE}}{S_{△ABF}} = (\frac{AC}{AB})^2 = \frac{1}{4}$（易错点：相似三角形的面积之比等于相似比的平方，勿弄错），
∴$S_{△ABF} = 4S_{△ACE}$，
∴$S_{四边形BCEF} = 7S_{△ACE}$，
∴$S_{△ACE}:S_{四边形BCEF} = 1:7$。 ×

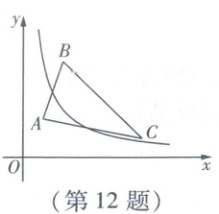
12. 如图，$\triangle ABC$的三个顶点分别为$A(1,2)$，$B(2,5)$，$C(6,1)$。若函数$y = \frac{k}{x}$在第一象限内的图象与$\triangle ABC$有交点，则$k$的取值范围是(A)

A.$2\leq k\leq\frac{49}{4}$
B.$6\leq k\leq10$
C.$2\leq k\leq6$
D.$2\leq k\leq\frac{25}{2}$

答案：
12A 当反比例函数y = $\frac{k}{x}$的图象过点A(1,2)时（临界位置1），如图中$L_1$，此时反比例函数的解析式为y = $\frac{2}{x}$。设直线BC的解析式为y = mx + n，将B(2,5)，C(6,1)分别代入，得$\begin{cases}2m + n = 5\\6m + n = 1\end{cases}$，解得$\begin{cases}m = -1\\n = 7\end{cases}$，
∴直线BC的解析式为y = -x + 7。
当反比例函数y = $\frac{k}{x}$的图象与直线y = -x + 7只有一个交点时（临界位置2），如图中$L_2$。令 -x + 7 = $\frac{k}{x}$，整理，得$x^2 - 7x + k = 0$，则Δ = 49 - 4k = 0，解得k = $\frac{49}{4}$。当k = $\frac{49}{4}$时，$x^2 - 7x + \frac{49}{4} = 0$，解得x = $\frac{7}{2}$（提示：
∵2 ＜ $\frac{7}{2}$ ＜ 6，
∴$L_2$与直线BC的交点在线段BC上）。分析可知，符合题意的k的取值范围为2 ≤ k ≤ $\frac{49}{4}$。

13. 计算$\sqrt{18}÷\sqrt{2}$的结果是3。

答案： 13 3

14. 点$A(1,-5)$关于原点的对称点的坐标为(-1,5)。

答案： 14 (-1,5)

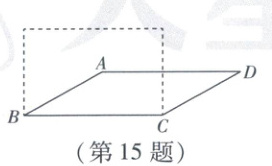
15. 如图，若将四根木条钉成的矩形木框变形为平行四边形$ABCD$的形状，并使其面积为矩形面积的一半，则这个平行四边形的一个最小内角的值等于30°。

答案：
15 30°
[解析]如图，过点A作AH⊥BC于点H。
∵平行四边形的面积是矩形面积的一半，
∴AH = $\frac{1}{2}$A'B = $\frac{1}{2}$AB，
∴∠ABH = 30°。

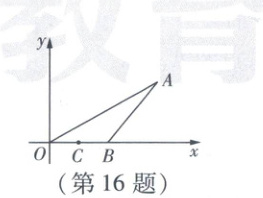
16. 如图，已知点$A$的坐标为$(\sqrt{3},1)$，$B$为$x$轴正半轴上一动点，$C$是$OB$的中点，则在点$B$运动的过程中，$AB + BC$的最小值为$\sqrt{3}$。

答案：
16 $\sqrt{3}$
快招解题法 试题秒解 考场速用
本题可利用“胡不归”模型求解：
∵C是OB的中点，
∴BC = $\frac{1}{2}$OB，
∴AB + BC = AB + $\frac{1}{2}$OB（注：符合“胡不归”模型）。如图
(1)，在x轴下方作∠BOM = 30°（第一步：作角，使sin∠BOM = $\frac{1}{2}$），过点B作BD⊥OM于点D，则BD = $\frac{1}{2}$OB，
∴AB + BC = AB + BD，
∴当A，B，D三点共线时，AB + BC的值最小（关键点）。如图
(2)，过点A作AD⊥OM于点D，交x轴于点B（第二步：作垂线），此时AB + BC的值最小，最小值为AD的长。过点A作AE⊥x轴于点E：
∵A($\sqrt{3}$,1)，
∴AE = 1，OE = $\sqrt{3}$，
∴tan∠AOE = $\frac{AE}{OE} = \frac{\sqrt{3}}{3}$，
∴∠AOE = 30°，
∴OA = 2AE = 2，∠AOD = 60°，
∴AD = OA·sin60° = 2×$\frac{\sqrt{3}}{2} = \sqrt{3}$，故AB + BC的最小值为$\sqrt{3}$。
巧作辅助线：将BC的长转化为BD的长，从而将求AB + BC的最小值，转化为求点A到直线OM的最短距离
　　　

17. （本小题满分7分）
已知整式$P = x^2 - 2(2x - x^2) + 1$。
（1）化简$P$；
（2）若$P = 0$，利用判别式判断此方程实数根的情况。

答案： 17
(1)P = $x^2 - 4x + 2x^2 + 1 = 3x^2 - 4x + 1$。(3分)
(2)当P = 0时，$3x^2 - 4x + 1 = 0$，(4分)
∴Δ = $(-4)^2 - 4×3×1 = 4 ＞ 0$，(6分)
∴此方程有两个不相等的实数根。(7分)