2026年金考卷中考45套汇编数学河北专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年金考卷中考45套汇编数学河北专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第65页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
22. (本小题满分9分)
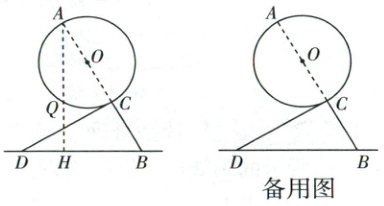
漆扇利用了漆不溶于水的特点制作而成. 淇淇把自己制作的圆形漆扇放在支架上,如图是其平面示意图,AC为圆形漆扇的直径,点O为圆心,扇柄BC = 10cm,且A,O,C,B在同一直线上,△BCD为支架,DC与⊙O相切于点C,BD = 20cm,点A到桌面的距离为AH,且AH与⊙O相交于点Q,点B与点H的距离BH = 13cm.
(1)求∠A的度数;
(2)求$\overgroup{QC}$的长度;
(3)不改变现有漆扇的大小和位置,直接写出点D到圆形漆扇边缘的最大距离.
漆扇利用了漆不溶于水的特点制作而成. 淇淇把自己制作的圆形漆扇放在支架上,如图是其平面示意图,AC为圆形漆扇的直径,点O为圆心,扇柄BC = 10cm,且A,O,C,B在同一直线上,△BCD为支架,DC与⊙O相切于点C,BD = 20cm,点A到桌面的距离为AH,且AH与⊙O相交于点Q,点B与点H的距离BH = 13cm.
(1)求∠A的度数;
(2)求$\overgroup{QC}$的长度;
(3)不改变现有漆扇的大小和位置,直接写出点D到圆形漆扇边缘的最大距离.

答案:
22
(1)
∵$DC$与$\odot O$相切于点$C$,$AC$为直径,
∴$CD\perp AB$(依据:切线的性质)。
在$Rt\triangle BCD$中,$BC = 10 cm$,$BD = 20 cm$,
∴$\sin\angle CDB = \frac{BC}{BD}=\frac{1}{2}$,
∴$\angle CDB = 30°$。
由题意知$AH\perp DB$,
∴$\angle AHB = \angle DCB = 90°$,
∴$\angle A = \angle CDB = 30°$。
(2)如图
(1),连接$OQ$。

由
(1)可知$\angle A = 30°$,
∴$\angle QOC = 60°$(依据:圆周角定理)。
在$Rt\triangle AHB$中,$\angle A = 30°$,$HB = 13 cm$,
∴$AB = 2BH = 26 cm$,
∴$AC = 26 - 10 = 16(cm)$,
∴$\odot O$的半径是$8$ cm,
∴$l_{弧QC}=\frac{60\pi×8}{180}=\frac{8\pi}{3}(cm)$。
(3)$(2\sqrt{91} + 8)cm$。
解法提示:如图
(2),连接$DO$并延长交$\odot O$于点$E$,过点$O$作$OG\perp BD$于点$G$,此时$DE$为点$D$到圆形漆扇边缘的最大距离。

在$Rt\triangle OBG$中,$\angle OBG = 60°$,$BO = BC + CO = 18 cm$,
∴$BG = \frac{1}{2}OB = 9 cm$,$OG = 9\sqrt{3} cm$,
∴$DG = BD - BG = 20 - 9 = 11(cm)$,
∴$OD = \sqrt{OG^2 + DG^2}=\sqrt{(9\sqrt{3})^2 + 11^2}=2\sqrt{91}(cm)$,
∴$DE = OD + OE = (2\sqrt{91} + 8)cm$,
∴点$D$到圆形漆扇边缘的最大距离为$(2\sqrt{91} + 8)cm$。
22
(1)
∵$DC$与$\odot O$相切于点$C$,$AC$为直径,
∴$CD\perp AB$(依据:切线的性质)。
在$Rt\triangle BCD$中,$BC = 10 cm$,$BD = 20 cm$,
∴$\sin\angle CDB = \frac{BC}{BD}=\frac{1}{2}$,
∴$\angle CDB = 30°$。
由题意知$AH\perp DB$,
∴$\angle AHB = \angle DCB = 90°$,
∴$\angle A = \angle CDB = 30°$。
(2)如图
(1),连接$OQ$。

由
(1)可知$\angle A = 30°$,
∴$\angle QOC = 60°$(依据:圆周角定理)。
在$Rt\triangle AHB$中,$\angle A = 30°$,$HB = 13 cm$,
∴$AB = 2BH = 26 cm$,
∴$AC = 26 - 10 = 16(cm)$,
∴$\odot O$的半径是$8$ cm,
∴$l_{弧QC}=\frac{60\pi×8}{180}=\frac{8\pi}{3}(cm)$。
(3)$(2\sqrt{91} + 8)cm$。
解法提示:如图
(2),连接$DO$并延长交$\odot O$于点$E$,过点$O$作$OG\perp BD$于点$G$,此时$DE$为点$D$到圆形漆扇边缘的最大距离。

在$Rt\triangle OBG$中,$\angle OBG = 60°$,$BO = BC + CO = 18 cm$,
∴$BG = \frac{1}{2}OB = 9 cm$,$OG = 9\sqrt{3} cm$,
∴$DG = BD - BG = 20 - 9 = 11(cm)$,
∴$OD = \sqrt{OG^2 + DG^2}=\sqrt{(9\sqrt{3})^2 + 11^2}=2\sqrt{91}(cm)$,
∴$DE = OD + OE = (2\sqrt{91} + 8)cm$,
∴点$D$到圆形漆扇边缘的最大距离为$(2\sqrt{91} + 8)cm$。
23. (本小题满分11分)
新定义 折线距离 定义:平面直角坐标系中,对于$E(x_1,y_1)$,$F(x_2,y_2)$两点,称$|x_1 - x_2| + |y_1 - y_2|$为E,F两点的“折线距离”,记为$G(EF)$.
【探究应用】
在平面直角坐标系中,已知$A(1,3)$,$B(4,4)$.
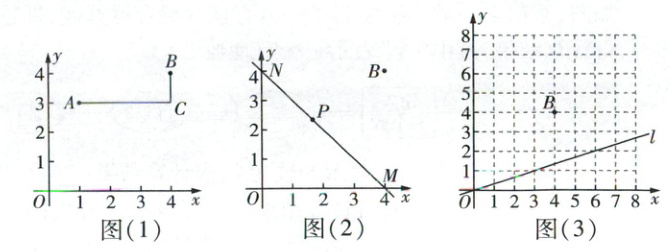
(1)如图(1),$AC // x$轴,$BC // y$轴,$G(AB) = AC + BC =$
(2)如图(2),一次函数$y = -x + 4$的图象与x轴交于点M,与y轴交于点N,在线段MN上任取一点P,$G(PB)$是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
【拓展延伸】
(3)如图(3),若点Q是直线$l:y_1 = \frac{1}{3}x$上一动点,直接画出满足$G(QB) ≤ 4$的所有点Q构成的线段,并直接写出此线段的长度.
(4)直接写出满足$G(RB) = 4$的所有点R围成图形的面积.
新定义 折线距离 定义:平面直角坐标系中,对于$E(x_1,y_1)$,$F(x_2,y_2)$两点,称$|x_1 - x_2| + |y_1 - y_2|$为E,F两点的“折线距离”,记为$G(EF)$.
【探究应用】
在平面直角坐标系中,已知$A(1,3)$,$B(4,4)$.
(1)如图(1),$AC // x$轴,$BC // y$轴,$G(AB) = AC + BC =$
4
.(2)如图(2),一次函数$y = -x + 4$的图象与x轴交于点M,与y轴交于点N,在线段MN上任取一点P,$G(PB)$是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
【拓展延伸】
(3)如图(3),若点Q是直线$l:y_1 = \frac{1}{3}x$上一动点,直接画出满足$G(QB) ≤ 4$的所有点Q构成的线段,并直接写出此线段的长度.
(4)直接写出满足$G(RB) = 4$的所有点R围成图形的面积.

答案:
23
(1)4
(2)$G(PB)$为定值。
如图
(1),过点$P$作$PD// x$轴,过点$B$作$BD// y$轴。

设$P(t,-t + 4)$,则$PD = 4 - t$,$BD = 4 - (-t + 4)=t$,
∴$G(PB)=PD + BD = 4 - t + t = 4$。
(3)如图
(2),$Q_1(3,1)$,$Q_2(6,2)$,线段$Q_1Q_2$即为所求。

∴点$Q$构成的线段长度为$\sqrt{(6 - 3)^2+(1 - 2)^2}=\sqrt{10}$。
解法提示:设$Q(n,\frac{1}{3}n)$,则$G(QB)=|n - 4|+|\frac{1}{3}n - 4|\leqslant4$。
令$n - 4 = 0$,解得$n = 4$;令$\frac{1}{3}n - 4 = 0$,解得$n = 12$。
分三种情况讨论(点拨:对应如图
(3)所示的三段)。

①当$n < 4$时(注:点$Q$在射线$EO$上),$n - 4 < 0$,$\frac{1}{3}n - 4 < 0$,
∴$4 - n - \frac{1}{3}n + 4\leqslant4$,解得$n\geqslant3$,
∴$3\leqslant n < 4$。
②当$4\leqslant n\leqslant12$时(注:点$Q$在线段$EF$上),$n - 4\geqslant0$,$\frac{1}{3}n - 4\leqslant0$,
∴$n - 4 - \frac{1}{3}n + 4\leqslant4$,解得$n\leqslant6$,
∴$4\leqslant n\leqslant6$。
③当$n > 12$时,易知$G(QB)>4$,故不符合题意。
综上,满足题意的点$Q$构成的线段为点$(3,1)$与点$(6,2)$的连线。
(4)32。
解法提示:设$R(x,y)$,则$G(RB)=|x - 4|+|y - 4|=4$,
当$x = 0$时,$y = 4$,则$R(0,4)$,
当$y = 0$时,$x = 4$,则$R(4,0)$,
当$x = 4$时,$y = 8$,则$R(4,8)$,
当$y = 4$时,$x = 8$,则$R(8,4)$,
∴满足$G(RB)=4$的点$R$围成的图形是以$B(4,4)$为中心的正方形,正方形的顶点为$(8,4)$,$(4,8)$,$(0,4)$,$(4,0)$,如图
(4)。

该正方形的对角线长为8,
∴该正方形的面积为$\frac{1}{2}×8×8 = 32$,
即满足$G(RB)=4$的所有点$R$围成图形的面积为32。
23
(1)4
(2)$G(PB)$为定值。
如图
(1),过点$P$作$PD// x$轴,过点$B$作$BD// y$轴。

设$P(t,-t + 4)$,则$PD = 4 - t$,$BD = 4 - (-t + 4)=t$,
∴$G(PB)=PD + BD = 4 - t + t = 4$。
(3)如图
(2),$Q_1(3,1)$,$Q_2(6,2)$,线段$Q_1Q_2$即为所求。

∴点$Q$构成的线段长度为$\sqrt{(6 - 3)^2+(1 - 2)^2}=\sqrt{10}$。
解法提示:设$Q(n,\frac{1}{3}n)$,则$G(QB)=|n - 4|+|\frac{1}{3}n - 4|\leqslant4$。
令$n - 4 = 0$,解得$n = 4$;令$\frac{1}{3}n - 4 = 0$,解得$n = 12$。
分三种情况讨论(点拨:对应如图
(3)所示的三段)。

①当$n < 4$时(注:点$Q$在射线$EO$上),$n - 4 < 0$,$\frac{1}{3}n - 4 < 0$,
∴$4 - n - \frac{1}{3}n + 4\leqslant4$,解得$n\geqslant3$,
∴$3\leqslant n < 4$。
②当$4\leqslant n\leqslant12$时(注:点$Q$在线段$EF$上),$n - 4\geqslant0$,$\frac{1}{3}n - 4\leqslant0$,
∴$n - 4 - \frac{1}{3}n + 4\leqslant4$,解得$n\leqslant6$,
∴$4\leqslant n\leqslant6$。
③当$n > 12$时,易知$G(QB)>4$,故不符合题意。
综上,满足题意的点$Q$构成的线段为点$(3,1)$与点$(6,2)$的连线。
(4)32。
解法提示:设$R(x,y)$,则$G(RB)=|x - 4|+|y - 4|=4$,
当$x = 0$时,$y = 4$,则$R(0,4)$,
当$y = 0$时,$x = 4$,则$R(4,0)$,
当$x = 4$时,$y = 8$,则$R(4,8)$,
当$y = 4$时,$x = 8$,则$R(8,4)$,
∴满足$G(RB)=4$的点$R$围成的图形是以$B(4,4)$为中心的正方形,正方形的顶点为$(8,4)$,$(4,8)$,$(0,4)$,$(4,0)$,如图
(4)。

该正方形的对角线长为8,
∴该正方形的面积为$\frac{1}{2}×8×8 = 32$,
即满足$G(RB)=4$的所有点$R$围成图形的面积为32。
查看更多完整答案,请扫码查看


