《2026年金考卷中考45套汇编数学河北专版》

22. （本小题满分9分）
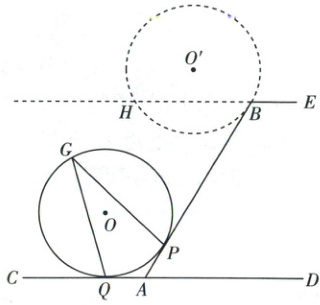
如图，斜坡$AB$与地面$CD$的夹角$\angle BAD = 60^{\circ}$，斜坡顶端$BE// CD$。半径为2的$\odot O$与$AB$相切于点$P$，与$CD$相切于点$Q$，$\odot O$上固定的一点$G$恰在$\angle BAC$的平分线上。某一时刻，$\odot O$带动点$G$沿斜坡$AB$向上滚动（无滑动），当$\odot O$与$AB$切于点$G$时停止滚动，发现此时点$G$恰与点$B$重合，此时圆心记为$O'$。
（1）当$\odot O$在初始位置时，求证：$\angle BAD = 2\angle PGQ$；
（2）求斜坡$AB$的长（结果保留$\pi$）；
（3）设$\odot O'$与$EB$的延长线交于另一点$H$，求$BH$的长。

答案：
22
(1)证明：如图，连接OP，OQ。
∵⊙O与AB相切于点P，与CD相切于点Q，
∴OP⊥AB，OQ⊥AC，
∴∠APO = ∠AQO = 90°。
∵∠POQ + ∠PAQ + ∠APO + ∠AQO = 360°（点拨：四边形的内角和为360°），
∴∠POQ + ∠PAQ = 180°。
又
∵∠BAD + ∠PAQ = 180°，
∴∠POQ = ∠BAD。
又
∵∠POQ = 2∠PGQ（依据：圆周角定理），
∴∠BAD = 2∠PGQ。(3分)

(2)如图，连接OA，AG。
∵∠APO = ∠AQO = 90°，OP = OQ，OA = OA，
∴Rt△OPA≌Rt△OQA（HL），
∴∠OAP = ∠OAQ，即AO平分∠PAQ。
∵∠BAD + ∠PAQ = 180°，∠BAD = 60°，
∴∠PAQ = 120°，
∴∠OAP = $\frac{1}{2}$∠PAQ = 60°。
∵tan∠OAP = $\frac{OP}{AP}$，
∴AP = $\frac{OP}{tan∠OAP} = \frac{2}{\sqrt{3}} = \frac{2\sqrt{3}}{3}$（关键点1：求出AP的长）。
∵点G恰在∠BAC的平分线上，
∴A，O，G三点共线，
∴∠POG = ∠OAP + ∠OPA = 60° + 90° = 150°，
∴PG的长为$\frac{150π×2}{180} = \frac{5π}{3}$，
∴BP = $\frac{5π}{3}$（关键点2：求出BP的长），
∴AB = AP + BP = $\frac{2\sqrt{3}}{3} + \frac{5π}{3}$。(6分)
(3)如图，连接O'B，过点O'作O'F⊥BH于F。
∵BE//CD，
∴∠ABH = ∠BAD = 60°。
∵⊙O'与AB相切，
∴∠O'BA = 90°，
∴∠O'BH = 30°，
∴BF = O'B·cos∠O'BF = 2cos30° = $\sqrt{3}$。
∵O'F⊥BH，
∴BH = 2BF = 2$\sqrt{3}$（依据：垂径定理）。(9分)

23. （本小题满分11分）
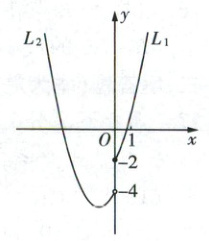
已知抛物线$L_1:y = x^2 - 2ax - 2(x\geq0)$，抛物线$L_2:y = x^2 - 2ax - 4(x ＜ 0)$，图象$L_1$与图象$L_2$组合成图象$G$。
（1）如图，当$a = -1$时。
①求图象$G$最低点的纵坐标；
②点$P(b,4)$在图象$G$上，求$b$的值。
（2）已知$A(0,-3)$，$B(\frac{3}{2},-3)$，当此图象$G$与线段$AB$只有一个公共点时，求$a$的取值范围。
（3）若图象$G$有且只有4个点到$x$轴的距离等于5，直接写出$a$的取值范围。

答案：
23
(1)①当a = -1时，抛物线$L_1:y = x^2 + 2x - 2 = (x + 1)^2 - 3$（x≥0），$L_2:y = x^2 + 2x - 4 = (x + 1)^2 - 5$（x＜0）。
a.当x≥0时，则当x = 0时，$L_1$有最小值 -2（点拨：当x≥ -1时，y随x的增大而增大）。
b.当x＜0时，则当x = -1时，$L_2$有最小值 -5。
∵ -2 ＞ -5，
∴图象G最低点的纵坐标为 -5。(3分)
②将P(b,4)代入y = $x^2 + 2x - 2$，得$b^2 + 2b - 2 = 4$，
解得$b_1 = -1 + \sqrt{7}$，$b_2 = -1 - \sqrt{7}$（不合题意，舍去）；
将P(b,4)代入y = $x^2 + 2x - 4$，得$b^2 + 2b - 4 = 4$，
解得$b_1 = -4$，$b_2 = 2$（不合题意，舍去）。
综上，b的值为 -1 + $\sqrt{7}$或 -4。(6分)
(2)
∵A(0, -3)，B($\frac{3}{2}$, -3)，图象G与线段AB只有一个公共点，
∴x ＞ 0，
∴抛物线$L_1:y = x^2 - 2ax - 2$（x≥0）与线段AB只有一个公共点（关键点）。
分析可知，分两种情况讨论：
①当抛物线$y = x^2 - 2ax - 2$与直线y = -3只有一个公共点时，令$x^2 - 2ax - 2 = -3$，
∴$x^2 - 2ax + 1 = 0$，
∴Δ = $(-2a)^2 - 4 = 0$，
解得a = 1或a = -1。
当a = -1时，交点为(-1, -3)，不合题意，舍去（忽略交点的横坐标大于0，从而误认为此种情况符合题意）；
当a = 1时，交点为(1, -3)，符合题意。
②当x = $\frac{3}{2}$，y ＜ -3时，
即$\frac{9}{4} - 3a - 2 ＜ -3$，
∴a ＞ $\frac{13}{12}$。
综上所述，当图象G与线段AB只有一个公共点时，a = 1或a ＞ $\frac{13}{12}$。(9分)
(3)a ＜ -1或a ＞ $\sqrt{3}$。(11分)
解法提示：
∵y = $x^2 - 2ax - 2 = (x - a)^2 - a^2 - 2$，y = $x^2 - 2ax - 4 = (x - a)^2 - a^2 - 4$，
∴抛物线$L_1$与抛物线$L_2$的对称轴均为直线x = a。
分析可知，分两种情况讨论：
①当a ＞ 0时，画出图象G的大致图象及直线y = ±5，如图
(1)所示。
易知当x≥0时，$y_{最小} = -a^2 - 2$；当x ＜ 0时，$y_{最小} ＞ -a^2 - 4$。
结合图象分析可知，若图象G有且只有4个点到x轴的距离等于5，则$-a^2 - 2 ＜ -5$（点拨：只需抛物线$L_1$在x轴下方的图象与直线y = -5有两个交点即可），
∴a ＞ $\sqrt{3}$（点拨：a ＜ -$\sqrt{3}$不符合a ＞ 0，已舍去）。

②当a ＜ 0时，画出图象G的大致图象及直线y = ±5，如图
(2)所示。
易知当x≥0时，$y_{最小} = -2$；当x ＜ 0时，$y_{最小} = -a^2 - 4$。
结合图象分析可知，若图象G有且只有4个点到x轴的距离等于5，则$-a^2 - 4 ＜ -5$（点拨：只需抛物线$L_2$在x轴下方的图象与直线y = -5有两个交点即可），
∴a ＜ -1（注：a ＞ 1不符合a ＜ 0，已舍去）。

综上所述，当a ＜ -1或a ＞ $\sqrt{3}$时，图象G有且只有4个点到x轴的距离等于5。