《2026年金考卷中考45套汇编数学河北专版》

26. （本小题满分12分）
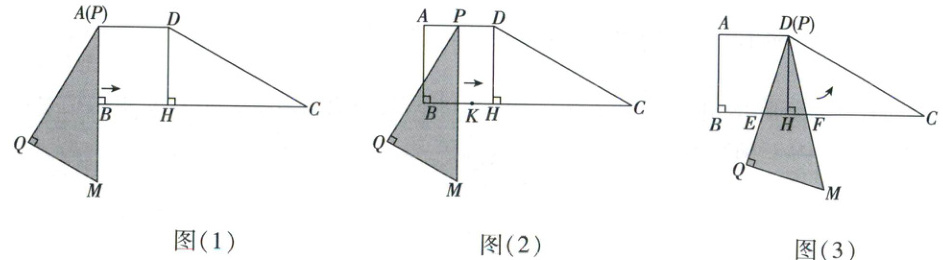
四边形$ABCD$中，$AD// BC$，$\angle ABC=90^{\circ}$，$\angle C=30^{\circ}$，$AD=3$，$AB=2\sqrt{3}$，$DH\perp BC$于点$H$. 将$\triangle PQM$与该四边形按如图（1）方式放在同一平面内，使点$P$与$A$重合，点$B$在$PM$上，其中$\angle Q=90^{\circ}$，$\angle QPM=30^{\circ}$，$PM=4\sqrt{3}$.
（1）求证：$\triangle PQM\cong\triangle CHD$.
（2）$\triangle PQM$从图（1）的位置出发，先沿着$BC$方向向右平移（图（2）），当点$P$到达点$D$后$\triangle PQM$立刻绕点$D$逆时针旋转（图（3）），当边$PM$旋转$50^{\circ}$时停止.
①从平移开始，到绕点$D$旋转结束，求边$PQ$扫过的面积.
②如图（2），点$K$在$BH$上，且$BK=9-4\sqrt{3}$. 若$\triangle PQM$右移的速度为每秒1个单位长，绕点$D$旋转的速度为每秒$5^{\circ}$，求点$K$在$\triangle PQM$区域（含边界）内的时长.
③如图（3），在$\triangle PQM$旋转过程中，设$PQ$，$PM$分别交$BC$于点$E$，$F$，若$BE=d$，直

接

写出$CF$的长（用含$d$的式子表示）.

答案：
26
(1)证明：$\because AD // BC$，$\angle ABC = 90^{\circ}$，$DH \perp BC$，$\therefore DH = AB = 2\sqrt{3}$.
$\because \angle DHC = 90^{\circ}$，$\angle C = 30^{\circ}$，$\therefore CD = 2DH = 4\sqrt{3}$.
在$\triangle PQM$和$\triangle CHD$中，$\angle PQM = \angle DHC$，$\angle QPM = \angle C$，$PM = CD$，$\therefore \triangle PQM \cong \triangle CHD$.
(2)①如图
(1)，过点$Q$作$QG \perp PM$于点$G$.
易知$AQ = AM · \cos 30^{\circ} = 6$，则$QG = \frac{1}{2}AQ = 3$，$AG = AQ · \cos 30^{\circ} = 3\sqrt{3}$.
设点$Q$的初始位置为点$Q^{\prime}$，点$P$平移至点$D$时，点$Q$对应的位置为点$Q^{\prime\prime}$. 如图
(2)，边$PQ$平移扫过了$□ AQ^{\prime}Q^{\prime\prime}D$，其面积为$AG · AD = 9\sqrt{3}$，边$PQ$绕点$D$旋转$50^{\circ}$，扫过了扇形$Q^{\prime\prime}DQ$，其面积为$\frac{50 × \pi × 6^{2}}{360} = 5\pi$，$\therefore$边$PQ$扫过的面积为$9\sqrt{3} + 5\pi$.


②如图
(3)，连接$DK$.
$\because CH = \frac{DH}{\tan 30^{\circ}} = 6$，$\therefore BC = BH + HC = 9$.
$\because BK = 9 - 4\sqrt{3}$，$\therefore CK = 4\sqrt{3} = CD$.
又$\because \angle C = 30^{\circ}$，$\therefore \angle KDC = \frac{180^{\circ} - 30^{\circ}}{2} = 75^{\circ}$.
$\because KH = CK - CH = 4\sqrt{3} - 6$，$\therefore PM$平移时从经过点$K$到经过点$H$，用时$(4\sqrt{3} - 6)$秒.
又旋转过程中点$K$在$\triangle PQM$区域内的时长为$\frac{60 + 30 - 75}{5} = 3$(秒)，$\therefore$所求时长为$(4\sqrt{3} - 3)$秒.
③$\frac{60 - 12d}{9 - d}$.
解法提示：当点$H$不在$PQ$上时，在$Rt \triangle DEH$中，由勾股定理，得$DE^{2} = EH^{2} + DH^{2} = (3 - d)^{2} + (2\sqrt{3})^{2}$.
易知$\angle DEF = \angle CED$，$\angle EDF = \angle C = 30^{\circ}$，$\therefore \triangle DEF \sim \triangle CED$，$\therefore \frac{DE}{CE} = \frac{EF}{ED}$，即$DE^{2} = EF · EC$，$\therefore (3 - d)^{2} + (2\sqrt{3})^{2} = EF · (9 - d)$，整理，得$EF = \frac{d^{2} - 6d + 21}{9 - d}$，$\therefore CF = BC - BE - EF = 9 - d - \frac{d^{2} - 6d + 21}{9 - d} = \frac{60 - 12d}{9 - d}$.
当点$H$在$PQ$上时，$d = 3$，$CF = 4$，符合$CF = \frac{60 - 12d}{9 - d}$.
综上可知，$CF = \frac{60 - 12d}{9 - d}$.