2026年金考卷中考45套汇编数学河北专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年金考卷中考45套汇编数学河北专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第113页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
22. (本小题满分9分)
新考法 折叠操作 【情境】
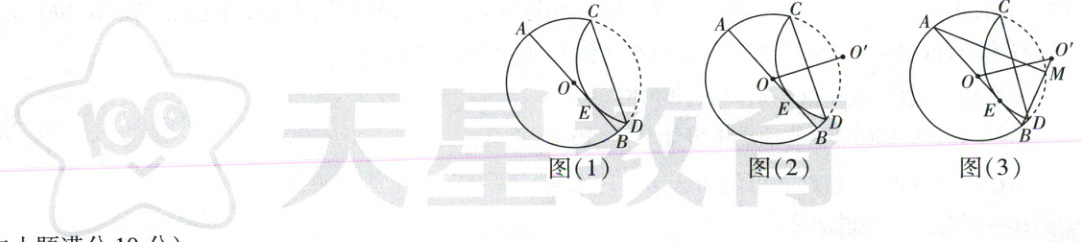
数学课上,同学们用圆形纸片探究折叠的性质,如图(1),$AB$是$\odot O$的直径,$AB = 4$,沿弦$CD$折叠,使折叠后的$\overset{\frown}{CD}$与$AB$相切于点$E$。
【发现】
$\overset{\frown}{CED}$所在圆的半径为
【探究】
为了找到$\overset{\frown}{CED}$所在圆的圆心,同学们讨论了以下两种方式。
淇淇说:取弦$CE$和弦$ED$的中垂线的交点即可。
嘉嘉说:不必画两条中垂线,如图(2),只需作点$O$关于直线$CD$的对称点$O'$,点$O'$即为所求。
淇淇说:这样看来,折叠后,切点$E$在线段$AB$上运动,可以看成$\odot O'$在线段$AB$上滚动。
嘉嘉说:没错,当点$E$在线段$AB$上运动时,点$O'$的运动路线和线段$AB$的位置关系是
【拓展】
(1)如图(3),若切点$E$为$OB$的中点,连接$O'B$,交$\odot O$于点$M$,连接$AM$,求弦$AM$的长;
(2)若切点$E$落在线段$OB$上(包括端点),直接写出$CD$的最大值和最小值。
新考法 折叠操作 【情境】
数学课上,同学们用圆形纸片探究折叠的性质,如图(1),$AB$是$\odot O$的直径,$AB = 4$,沿弦$CD$折叠,使折叠后的$\overset{\frown}{CD}$与$AB$相切于点$E$。
【发现】
$\overset{\frown}{CED}$所在圆的半径为
2
。【探究】
为了找到$\overset{\frown}{CED}$所在圆的圆心,同学们讨论了以下两种方式。
淇淇说:取弦$CE$和弦$ED$的中垂线的交点即可。
嘉嘉说:不必画两条中垂线,如图(2),只需作点$O$关于直线$CD$的对称点$O'$,点$O'$即为所求。
淇淇说:这样看来,折叠后,切点$E$在线段$AB$上运动,可以看成$\odot O'$在线段$AB$上滚动。
嘉嘉说:没错,当点$E$在线段$AB$上运动时,点$O'$的运动路线和线段$AB$的位置关系是
平行
。【拓展】
(1)如图(3),若切点$E$为$OB$的中点,连接$O'B$,交$\odot O$于点$M$,连接$AM$,求弦$AM$的长;
(2)若切点$E$落在线段$OB$上(包括端点),直接写出$CD$的最大值和最小值。

答案:
【发现】2 (1分)
【探究】平行 (3分)
解法提示:$\because \odot O'$与AB相切于点E,$\therefore O'E \perp AB$.
又$\because O'E = 2$,$\therefore$点O'的运动路线和线段AB平行.
【拓展】
(1)如图
(1),连接$O'E$.
$\because \odot O'$与AB相切于点E,$\therefore \angle O'EB = 90^{\circ}$(依据:切线的性质).
巧作辅助线:见相切,连半径,得垂直
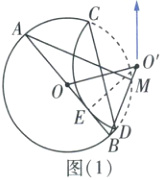
$\because$点M在$\odot O$上,AB为$\odot O$的直径,$\therefore \angle AMB = 90^{\circ}$(依据:直径所对的圆周角是直角).
在$\triangle AMB$和$\triangle O'EB$中,$\angle AMB = \angle O'EB$,$\angle ABM = \angle O'BE$,$\therefore \triangle AMB \backsim \triangle O'EB$,$\therefore \frac{AM}{AB} = \frac{O'E}{O'B}$
$\because E$为OB的中点,$OB = 2$,$\therefore EB = 1$.
又$\because O'E = 2$,$\therefore O'B = \sqrt{O'E^{2} + E'B^{2}} = \sqrt{5}$,$\therefore \frac{AM}{4} = \frac{2}{\sqrt{5}}$,$\therefore AM = \frac{8\sqrt{5}}{5}$. (7分)
(2)最大值为$2\sqrt{3}$,最小值为$2\sqrt{2}$. (9分)
解法提示:如图
(2),设$OO'$与CD交于点H,连接OC,$O'E$.
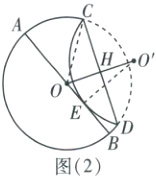
设$OE = x$,则$OO' = \sqrt{OE^{2} + O'E^{2}} = \sqrt{x^{2} + 4}$.
$\because$点O,$O'$关于直线CD对称,$\therefore OO' \perp CD$,$OH = O'H = \frac{1}{2}OO' = \frac{1}{2}\sqrt{x^{2} + 4}$,$\therefore DH = CH = \sqrt{OC^{2} - OH^{2}} = \sqrt{3 - \frac{x^{2}}{4}}$,$\therefore CD = 2CH = \sqrt{12 - x^{2}}$(关键点:用含x的式子表示CD的长).
$\because$点E在线段OB上,$\therefore 0 \leq x \leq 2$,$\therefore 2\sqrt{2} \leq CD \leq 2\sqrt{3}$,$\therefore CD$的最大值为$2\sqrt{3}$,最小值为$2\sqrt{2}$.
一题多解
第
(2)题还可以先找出CD取最大值和最小值时的位置,再求解,如下:
如图
(1),当点E与点0重合时,CD最长,此时点D'在$OO'$上,
设$OO'$与CD交于点H,连接OC.
$\because$点O,$O'$关于直线CD对称,
$\therefore OO' \perp CD$,$OH = O'H = \frac{1}{2}OO' = 1$,
$\therefore DH = CH = \sqrt{OC^{2} - OH^{2}} = \sqrt{3}$,$CD = 2\sqrt{3}$;


如图
(2),当点E与点B重合时,CD最短,此时点D也与点B重合.
连接$O'B$,$OC$,则$\angle OBO' = 90^{\circ}$.
由对称知BC平分$\angle OBO'$,
$\therefore \angle OBC = \frac{1}{2}\angle OBO' = 45^{\circ}$,由此易得$\angle BOC = 90^{\circ}$,$CD = \sqrt{2}OC = 2\sqrt{2}$.
综上,CD的最大值为$2\sqrt{3}$,最小值为$2\sqrt{2}$.
【发现】2 (1分)
【探究】平行 (3分)
解法提示:$\because \odot O'$与AB相切于点E,$\therefore O'E \perp AB$.
又$\because O'E = 2$,$\therefore$点O'的运动路线和线段AB平行.
【拓展】
(1)如图
(1),连接$O'E$.
$\because \odot O'$与AB相切于点E,$\therefore \angle O'EB = 90^{\circ}$(依据:切线的性质).
巧作辅助线:见相切,连半径,得垂直

$\because$点M在$\odot O$上,AB为$\odot O$的直径,$\therefore \angle AMB = 90^{\circ}$(依据:直径所对的圆周角是直角).
在$\triangle AMB$和$\triangle O'EB$中,$\angle AMB = \angle O'EB$,$\angle ABM = \angle O'BE$,$\therefore \triangle AMB \backsim \triangle O'EB$,$\therefore \frac{AM}{AB} = \frac{O'E}{O'B}$
$\because E$为OB的中点,$OB = 2$,$\therefore EB = 1$.
又$\because O'E = 2$,$\therefore O'B = \sqrt{O'E^{2} + E'B^{2}} = \sqrt{5}$,$\therefore \frac{AM}{4} = \frac{2}{\sqrt{5}}$,$\therefore AM = \frac{8\sqrt{5}}{5}$. (7分)
(2)最大值为$2\sqrt{3}$,最小值为$2\sqrt{2}$. (9分)
解法提示:如图
(2),设$OO'$与CD交于点H,连接OC,$O'E$.

设$OE = x$,则$OO' = \sqrt{OE^{2} + O'E^{2}} = \sqrt{x^{2} + 4}$.
$\because$点O,$O'$关于直线CD对称,$\therefore OO' \perp CD$,$OH = O'H = \frac{1}{2}OO' = \frac{1}{2}\sqrt{x^{2} + 4}$,$\therefore DH = CH = \sqrt{OC^{2} - OH^{2}} = \sqrt{3 - \frac{x^{2}}{4}}$,$\therefore CD = 2CH = \sqrt{12 - x^{2}}$(关键点:用含x的式子表示CD的长).
$\because$点E在线段OB上,$\therefore 0 \leq x \leq 2$,$\therefore 2\sqrt{2} \leq CD \leq 2\sqrt{3}$,$\therefore CD$的最大值为$2\sqrt{3}$,最小值为$2\sqrt{2}$.
一题多解
第
(2)题还可以先找出CD取最大值和最小值时的位置,再求解,如下:
如图
(1),当点E与点0重合时,CD最长,此时点D'在$OO'$上,
设$OO'$与CD交于点H,连接OC.
$\because$点O,$O'$关于直线CD对称,
$\therefore OO' \perp CD$,$OH = O'H = \frac{1}{2}OO' = 1$,
$\therefore DH = CH = \sqrt{OC^{2} - OH^{2}} = \sqrt{3}$,$CD = 2\sqrt{3}$;


如图
(2),当点E与点B重合时,CD最短,此时点D也与点B重合.
连接$O'B$,$OC$,则$\angle OBO' = 90^{\circ}$.
由对称知BC平分$\angle OBO'$,
$\therefore \angle OBC = \frac{1}{2}\angle OBO' = 45^{\circ}$,由此易得$\angle BOC = 90^{\circ}$,$CD = \sqrt{2}OC = 2\sqrt{2}$.
综上,CD的最大值为$2\sqrt{3}$,最小值为$2\sqrt{2}$.
23. (本小题满分10分)
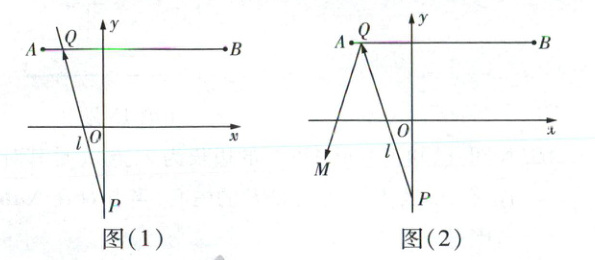
新课标 跨学科试题 已知点$A(-3,a)$,点$B(a + 2,a)$,其中$a > -5$。一束光从点$P(0,-4)$沿直线$y = kx + b$发出,形成的光线$l$与线段$AB$交于点$Q$,若点$Q$为整数点(横、纵坐标都为整数的点),则光线$l$穿过线段$AB$得到图(1),否则光线$l$在点$Q$处被反射得到射线$QM$(说明:反射角 = 入射角),进而得到图(2)。
(1)若点$Q$的坐标为$(-\frac{5}{2},4)$,
① 求直线$y = kx + b$的解析式(不必写自变量的取值范围)。
② 射线$QM$是否经过点$(-3,2)$?请说明理由。
(2)若$a = 3$,且$AB$上的整数点被点$Q$分为个数之比为$2:7$的两部分,求$k$的取值范围。
(3)若光线$l$穿过线段$AB$,且$k$为正整数,点$Q$为$AB$的中点,直接写出此时满足条件的整数$a$的个数。
新课标 跨学科试题 已知点$A(-3,a)$,点$B(a + 2,a)$,其中$a > -5$。一束光从点$P(0,-4)$沿直线$y = kx + b$发出,形成的光线$l$与线段$AB$交于点$Q$,若点$Q$为整数点(横、纵坐标都为整数的点),则光线$l$穿过线段$AB$得到图(1),否则光线$l$在点$Q$处被反射得到射线$QM$(说明:反射角 = 入射角),进而得到图(2)。
(1)若点$Q$的坐标为$(-\frac{5}{2},4)$,
① 求直线$y = kx + b$的解析式(不必写自变量的取值范围)。
② 射线$QM$是否经过点$(-3,2)$?请说明理由。
(2)若$a = 3$,且$AB$上的整数点被点$Q$分为个数之比为$2:7$的两部分,求$k$的取值范围。
(3)若光线$l$穿过线段$AB$,且$k$为正整数,点$Q$为$AB$的中点,直接写出此时满足条件的整数$a$的个数。

答案:
(1)①$\because$直线$y = kx + b$经过点$P(0, - 4)$,$Q( - \frac{5}{2},4)$,$\therefore b = - 4$,$ - \frac{5}{2}k + b = 4$,$\therefore \begin{cases} b = - 4, \\ - \frac{5}{2}k + b = 4, \end{cases} \therefore \begin{cases} k = - \frac{16}{5}, \\ b = - 4, \end{cases}$$\therefore$直线$y = kx + b$的解析式为$y = - \frac{16}{5}x - 4$. (3分)
②不经过. (4分)
理由:由题意知直线PQ与直线QM关于直线$x = - \frac{5}{2}$对称,$\therefore$点$P(0, - 4)$关于直线$x = - \frac{5}{2}$的对称点$P'( - 5, - 4)$在直线QM上.
设射线QM的解析式为$y = mx + n$,
将$( - 5, - 4)$,$( - \frac{5}{2},4)$分别代入,
得$\begin{cases} - 4 = - 5m + n, \\ 4 = - \frac{5}{2}m + n, \end{cases}$解得$\begin{cases} m = \frac{16}{5}, \\ n = 12, \end{cases}$
$\therefore$射线QM的解析式为$y = \frac{16}{5}x + 12(x \leq - \frac{5}{2})$.
当$x = - 3$时,$y = \frac{16}{5} × ( - 3) + 12 = \frac{12}{5} \neq 2$,$\therefore$射线QM不经过点$( - 3,2)$. (6分)
(2)当$a = 3$时,点$A( - 3,3)$,点$B(5,3)$,$\therefore$线段AB上的整数点有$( - 3,3)$,$( - 2,3)$,$( - 1,3)$,$(0,3)$,$(1,3)$,$(2,3)$,$(3,3)$,$(4,3)$,$(5,3)$,共9个.
$\because$AB上的整数点被点Q分为个数之比为2:7的两部分,$\therefore$点Q在$( - 2,3)$和$( - 1,3)$之间或在$(3,3)$和$(4,3)$之间.
$\because$直线l经过点$P(0, - 4)$,$\therefore$直线l的解析式为$y = kx - 4$.
将$( - 2,3)$代入$y = kx - 4$,得$k = - \frac{7}{2}$;
将$( - 1,3)$代入$y = kx - 4$,得$k = - 7$;
将$(3,3)$代入$y = kx - 4$,得$k = \frac{7}{3}$;
将$(4,3)$代入$y = kx - 4$,得$k = \frac{7}{4}$;
故k的取值范围为$- 7 < k < - \frac{7}{2}$或$\frac{7}{4} < k < \frac{7}{3}$ (8分)
(3)满足条件的整数a的个数为2. (10分)
解法提示:$\because$点Q为线段AB的中点,$\therefore Q(\frac{a - 1}{2},a)$.
将$(\frac{a - 1}{2},a)$代入直线$y = kx - 4$,
得$a = \frac{a - 1}{2} × k - 4$,解得$k = \frac{2a + 8}{a - 1} = 2 + \frac{10}{a - 1}$.
$\because k$为正整数,$a > - 5$且a为整数,且点Q为整数点,$\therefore$列表如下(点拨:先根据$\frac{10}{a - 1}$是整数,得到其可能是1,2,5,10,再求出相应的a,$\frac{a - 1}{2}$的值,当三者的值均为整数时即符合题意):
$\frac{10}{a - 1}$ 1 2 5 10
a 11 6 3 2
$\frac{a - 1}{2}$ 5 2.5 1 0.5
k 3 4 7 12
$\therefore a = 11$或3,即满足条件的整数a的个数为2.
(1)①$\because$直线$y = kx + b$经过点$P(0, - 4)$,$Q( - \frac{5}{2},4)$,$\therefore b = - 4$,$ - \frac{5}{2}k + b = 4$,$\therefore \begin{cases} b = - 4, \\ - \frac{5}{2}k + b = 4, \end{cases} \therefore \begin{cases} k = - \frac{16}{5}, \\ b = - 4, \end{cases}$$\therefore$直线$y = kx + b$的解析式为$y = - \frac{16}{5}x - 4$. (3分)
②不经过. (4分)
理由:由题意知直线PQ与直线QM关于直线$x = - \frac{5}{2}$对称,$\therefore$点$P(0, - 4)$关于直线$x = - \frac{5}{2}$的对称点$P'( - 5, - 4)$在直线QM上.
设射线QM的解析式为$y = mx + n$,
将$( - 5, - 4)$,$( - \frac{5}{2},4)$分别代入,
得$\begin{cases} - 4 = - 5m + n, \\ 4 = - \frac{5}{2}m + n, \end{cases}$解得$\begin{cases} m = \frac{16}{5}, \\ n = 12, \end{cases}$
$\therefore$射线QM的解析式为$y = \frac{16}{5}x + 12(x \leq - \frac{5}{2})$.
当$x = - 3$时,$y = \frac{16}{5} × ( - 3) + 12 = \frac{12}{5} \neq 2$,$\therefore$射线QM不经过点$( - 3,2)$. (6分)
(2)当$a = 3$时,点$A( - 3,3)$,点$B(5,3)$,$\therefore$线段AB上的整数点有$( - 3,3)$,$( - 2,3)$,$( - 1,3)$,$(0,3)$,$(1,3)$,$(2,3)$,$(3,3)$,$(4,3)$,$(5,3)$,共9个.
$\because$AB上的整数点被点Q分为个数之比为2:7的两部分,$\therefore$点Q在$( - 2,3)$和$( - 1,3)$之间或在$(3,3)$和$(4,3)$之间.
$\because$直线l经过点$P(0, - 4)$,$\therefore$直线l的解析式为$y = kx - 4$.
将$( - 2,3)$代入$y = kx - 4$,得$k = - \frac{7}{2}$;
将$( - 1,3)$代入$y = kx - 4$,得$k = - 7$;
将$(3,3)$代入$y = kx - 4$,得$k = \frac{7}{3}$;
将$(4,3)$代入$y = kx - 4$,得$k = \frac{7}{4}$;
故k的取值范围为$- 7 < k < - \frac{7}{2}$或$\frac{7}{4} < k < \frac{7}{3}$ (8分)
(3)满足条件的整数a的个数为2. (10分)
解法提示:$\because$点Q为线段AB的中点,$\therefore Q(\frac{a - 1}{2},a)$.
将$(\frac{a - 1}{2},a)$代入直线$y = kx - 4$,
得$a = \frac{a - 1}{2} × k - 4$,解得$k = \frac{2a + 8}{a - 1} = 2 + \frac{10}{a - 1}$.
$\because k$为正整数,$a > - 5$且a为整数,且点Q为整数点,$\therefore$列表如下(点拨:先根据$\frac{10}{a - 1}$是整数,得到其可能是1,2,5,10,再求出相应的a,$\frac{a - 1}{2}$的值,当三者的值均为整数时即符合题意):
$\frac{10}{a - 1}$ 1 2 5 10
a 11 6 3 2
$\frac{a - 1}{2}$ 5 2.5 1 0.5
k 3 4 7 12
$\therefore a = 11$或3,即满足条件的整数a的个数为2.
查看更多完整答案,请扫码查看


